Research areas

Our research interest mainly lies in the area of condensed-matter physics and statistical physics. We try to model various many-body phenomena in the nature and analyze the models by means of statistical mechanics, field theory, computer simulations, etc. Abstract models can describe seemingly unrelated phenomena in a unified way; this is the most powerful aspect of statistical physics. The following is a list of research areas in which we are currently working or are planning to work. The list should and will change constantly. We welcome your intersting suggestions.

Non-Hermitian Quantum Mechanics and Localization Phenomena
Although Hamiltonians in quantum mechanics are Hermitian operators, artificial non-Hermitian Hamiltonians can describe physica phenomena effectively. A localization transition of a system with non-Hermitian vector potential and random scalar potential corresponds to a pinning transition of magnetic flux lines in superconductors and provides a novel viewpoint of Hermitian localization.

Conduction of Mesoscopic Systems
Conduction of mesoscopic systems is affected by various elements such as localization and resonance. We are interested in treating the conduction from the point of view of the non-Hermitian quantum mechanics, in particular, the resonant conduction, which has huge peaks in the conductance curve.

Statistical Mechanics of Financial Phenomena
In recent years, there appeared studies that analyzes models of human activities such as financial market price. These studies have great impact on understanding of "many-body" phenomena, which have relied on instinctive skills. In particular, the source of fractal flucutation of stock price is of physical interest.

Statistical Mechanics of Directed Networks
It has benn found that various networks in social systems have a particular aspect of fractal nature. Several models have been proposed to treat such networks statistical mechanically. We are particularly interested in such networks with directed links.

Nonequilibrium Quantum Statistical Physics

Quantum Information Theory

Foundation of Quantum Mechanics

Non-Hermitian Quantum Mechanics

Nonequilibrium (Classical) Statistical Physics

(Equilibrium) Quantum Statistical Physics

Equilibrium Classical Statistical Physics

Entanglement generation dynamics in quantum heat engines (Ryohei Suzuki)

By defining operations such as manipulation of energy levels and interactions, we can regard small quantum systems, such as interacting spins, as quantum heat engines that extract work from reservoirs. General interacting quantum systems may have non-local correlation called entanglement, and indeed it has been reported that quantum heat engines generate entanglement between working spin and reservoirs. We are theoretically studying the relationship between the thermodynamic properties of quantum heat engines, such as thermal efficiency, and the dynamics of entanglement generation during their thermal cycles.

Top

Thermodynamics of Mesoscopic Thermoelectric Heat Engines (Kaoru Yamamoto)

Although heat engines are commonly assumed to be cyclic (i.e., after a sequence of operations, return to its original state, such as the Carnot cycle), steady-state systems such as thermoelectric devices can also act as heat engines. Specifically, mesoscopic (nano- to microscale) thermoelectric heat engines are widely studied from both theoretical and applicational points of view, partly due to its prospective high-efficiency, and also due to the interesting interplay between thermodynamics and quantum effects.

Computation of the thermal efficiency of such mesoscopic thermoelectric devices entails defining heat current. However, the conventional definition of heat current is not necessarily founded on solid ground.

In this resesarch, we reexamined the definition of heat current from a thermodynamical point of view by considering a heat engine in a nonequilibrium steady state (Fig. 1). We also demonstrated the reasonability of our new definition in regards of its entropy production, in which we conducted the computation by applying the Landauer formula (a foumula used for computing current in mesoscopic systems). We also discussed the sufficient and necessary condition for it to attain the Carnot efficiency.

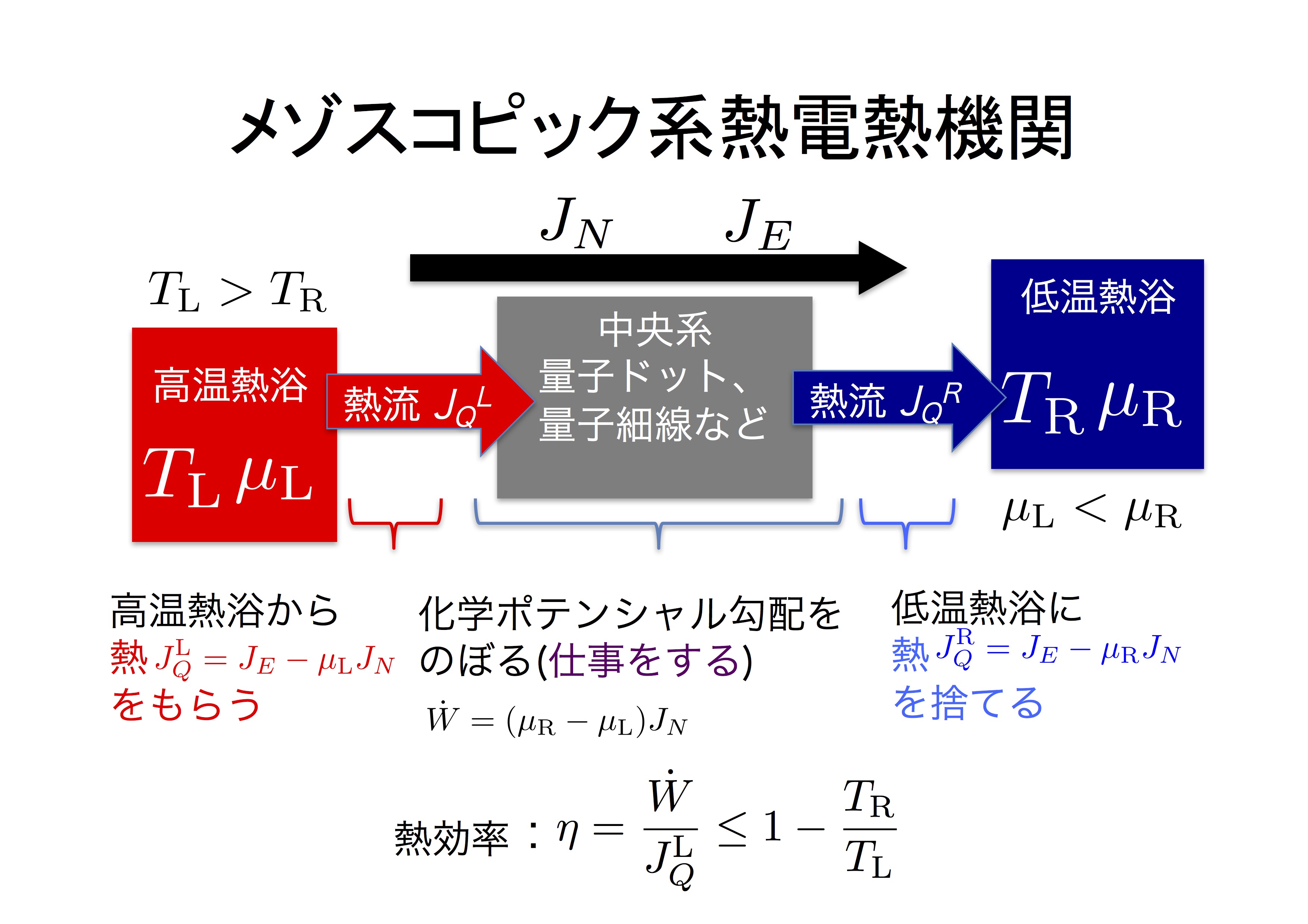
Fig. 1

References

  1. K. Yamamoto and N. Hatano, Phys. Rev. E 92, 042165 (2015).

Top

Non-markovianity in the time evolution of lattice quantum systems (Atsuki Yoshinaga)

Time evolution of a quantum system coupled to another system generally depends on the system’s history. We can attribute this feature to information backflow via environment, i.e. past information that flowed out of the system flows back later. In lattice quantum systems in which each site interacts only with its neighbors, there is a known upper limit to the speed with which information that flowed out of the system can propagate. We are analyzing how the time evolution of a subsystem of a lattice quantum system depends on surrounding’s state and the subsystem’s state in the past.

Top

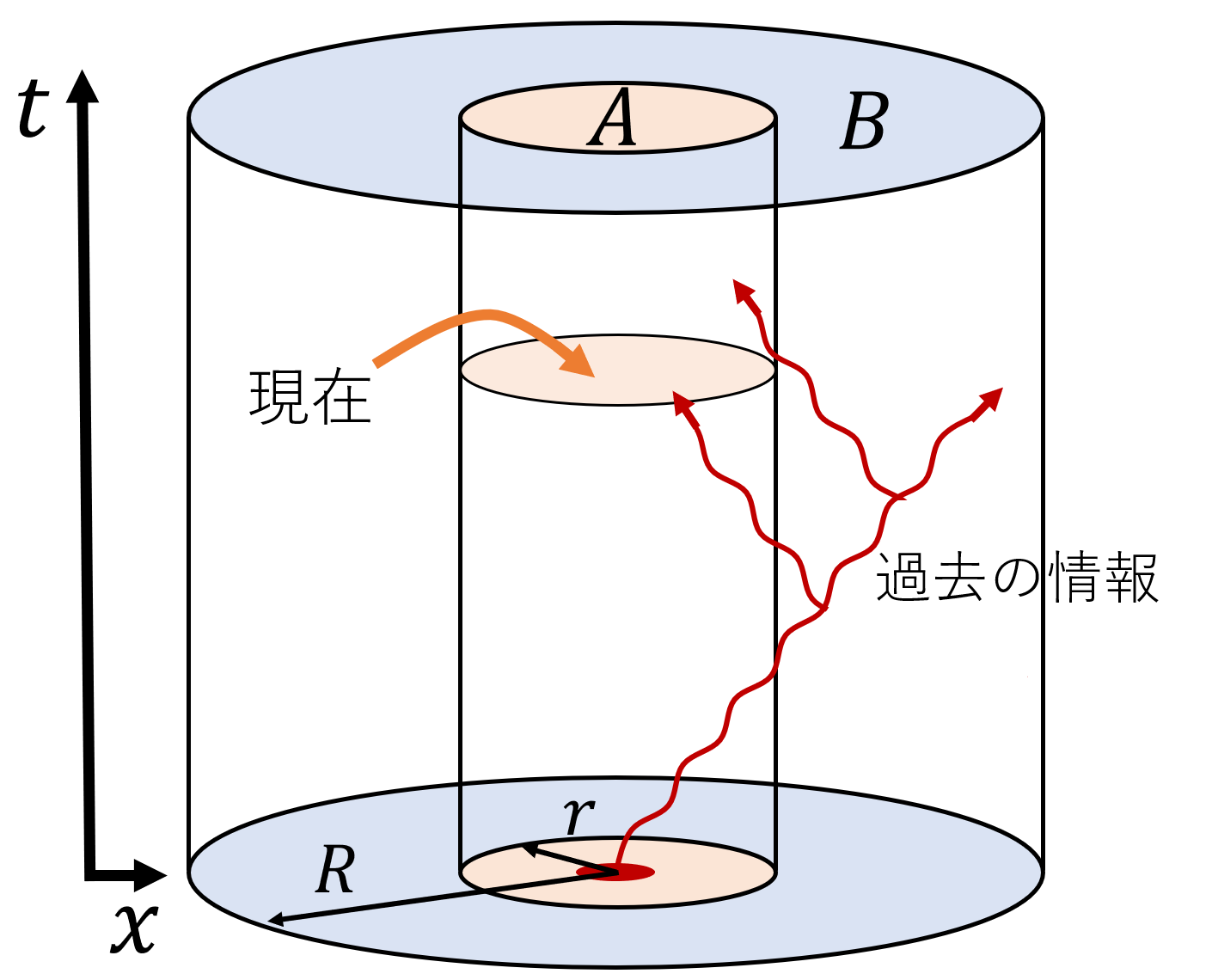
Quantum Thermodynamics of Gaussian States (Takaaki Aoki)

In recent years, due to the development of nanotechnology, research on thermodynamics of microscopic quantum systems has become more and more active. This research field is called quantum thermodynamics and is known that quantum thermodynamics is strongly related to quantum information. In the field of quantum information, Gaussian states are attracting much attention because they can be prepared and manipulated easily in experiments. In our research, we investigate the interaction dynamics of two Gaussian states using a quantum master equation and intend to define the heat and work exchanged between them so that they may be consistent with laws of thermodynamics.

Top

Geometric Formulation of Uncertainty Relations (Jaeha Lee)

References

  1. J. Lee and I. Tsutsui, Phys. Lett. A, 380: 2045-2048 (2016).
  2. K. Takeuchi, J. Lee, and I. Tsutsui, in preparation.

Top

Quantisation of Classical Observables and Quasi-probabilities in Quantum Mechanics (Jaeha Lee)

References

  1. J. Lee and I. Tsutsui, Prog. Theor. Exp. Phys. 2017 (5): 052A01 (2017).
  2. J. Lee and I. Tsutsui, Reality and Measurement in Algebraic Quantum Theory, 195-228, Springer Verlag (2018).

Top

Theoretical Analysis on the Applicability of Weak Measurement to Precision Measurement (Jaeha Lee)

References

  1. J. Lee and I. Tsutsui, Quantum Stud.: Math. Found., 1:65 (2014).
  2. Y. Mori, J. Lee, and I. Tsutsui, arXiv:1901.06831.

Top

Arrow of Times in Quantum Mechanics (Naomichi Hatano)

Except for the "weak interaction," all fundamental equations of motion in our world are time-reversal symmetric. Nonetheless, we are surrounded by time-irreversible phenomena in which specific events happen more often than the time-reversal events as time passes. Excited states decay and the entropy increases along the time. This type of irreversibility is called "arrow of time." We revealed why an arrow of time appears in the Schrödinger dynamics of quantum mechanics.

First, for open quantum systems (in which a finite system, such as a quantum dot, is attached with infinite systems, such as an infinitely long quantum lead) we discovered a novel complete set that is formed by all point spectra. The complete set is time-reversal symmetric, reflecting the time-reversal symmetry of the original Schrödinger.

Next, we expanded the time-evolution operator in terms of our new complete set. We thereby found that the excited state decays when we consider the initial condition problem, while the system grows up to the excited state when we consider the terminal condition problem (in which we specify the final state and ask what dynamics leads to the state).

References

  1. N. Hatano and G. Ordonez, J. Math. Phys. 55, 122106 (2014).

Top

Can we define the tunneling time? (Naomichi Hatano)

In quantum mechanics, we know the tunneling effect, in which a particle goes through an energy barrier. What time does it take a particle to go through the barrier? Can we actually define such a time? <\p>

This is a big issue that has been discussed by many researchers. We recently obtained two answers. On one hand, when the particle energy is far from the branch point at the energy band edge, we can define the tunneling time as the weighted average of the lifetime of resonant states. On the other hand, when the particle energy is close to the branch point, it turns out that it is in principle impossible to define the time properly. In the former case, we can find a characteristic time because the tunneling probability decays exponentially, while in the latter case, we cannot because it decays algebraically.

References

  1. G. Ordonez and N. Hatano, Phys. Rev. B 79 (2009) 042102.

Top

Definition and analysses of quantum-mechanical resonant state (Naomichi Hatano)

Many textbooks of quantum mechanics regard the resonant state phenomenologically, claiming that it is convenient to consider it as a state with a complex eigenvalue. In fact, we can rigorously define the resonant state as an eigenstate of the Schrödinger equation of open quantum systems. Its eigenfunction decays in time because of a negative imaginary part of the eigenvalue but diverges in space because of the negative imaginary part of the eigen-wave-number. It appears to be unphysical and is indeed often called so, but we can argue that the state observes the particle-number conservation (Figure).

References

  1. N. Hatano, K. Sasada, H. Nakamura and T. Petrosky, Prog. Theor. Phys. 119 (2008) 187-222.

Top

Non-Hermitian Extension of the Anderson Localization (Naomichi Hatano)

When we increase the impurity concentration in a metal, it transitions into an insulator at a critical concentration. This is because an electron wave cannot conduct owing to scattering at impurities, just like a water wave cannot go forward owing to scattering at poles. This phenomenon is called the Anderson localization. Whether the electron wave is localized in space or not and, if localized how strongly so, depends on the impurity concentration and the electron energy.

In order to judge the localization, we proposed a novel non-Hermitian model, which is often called the Hatano-Nelson model. We introduced an imaginary vector potential to a metalic model with impurities, making the model non-Hermitian. The distribution of the complex eigenvalues (figure) of this intentionally non-Hermitized Hamiltonian tells us how the electron wave is localized in the original Hermitian model.

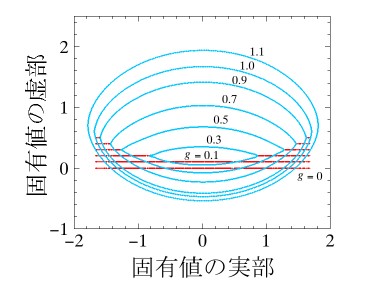
References

  1. N. Hatano and D.R. Nelson, Phys. Rev. Lett. 77 (1996) 570-573.

Top

Discrete-time quantum walk on complex networks for community detection (Kanae Mukai)

We define the discrete-time quantum walk on complex networks and utilize it for community detection. We numerically show that the quantum walk is localized in a community to which the initial node belongs. The infinite-time average of the normalized transition probability between two nodes, calculated from the eigenvectors, reveals the community structure, indicating that the eigenvectors contain information about localization to communities. We also find that the infinite-time average reveals the community structure better if the eigenvalues of the time-evolution unitary matrix are non-degenerate, and hence the Fourier walk is more suitable for community detection than the Grover walk. Meanwhile, the probability of the classical random walk on the same network quickly converges to a stationary distribution. We thus claim that the time average of the probability of the quantum walk on complex networks reveals the community structure more explicitly than that of the classical random walk.

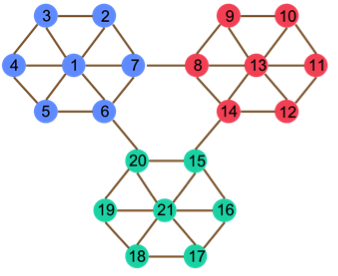
Fig. (a)

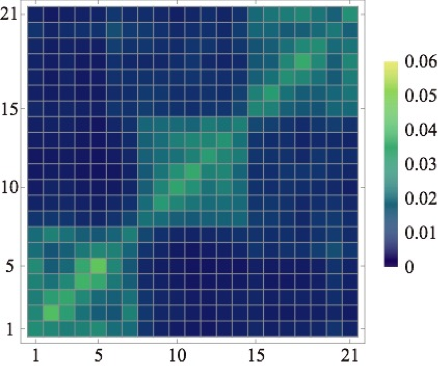
Fig. (b)

Fig. (a) is a prototypical three-community network. The hubs are the nodes 1, 13, and 21. Fig. (b) is the infinite-time average of the normalized transition probability of the Fourier walk on the three-community network. The vertical axis shows the initial node and the horizontal axis shows the final node.

Top

Effects of Boundary Conditions on Magnetic Friction (Kentaro Sugimoto)

Several experimental/theoretical/computational results support the existence of novel frictional phenomena with non-macroscopic degrees of freedom, multiple sliding surfaces, non-contact interaction, and so on, while our traditional image tells that "friction" occurs only in macroscopic systems in contact.

We considered two-dimensional Ising spin systems with two fixed boundary conditions and investigated the dependence of the distance between two boundaries and the temperature (Fig. 1). We use as fixed boundary conditions, the anti-parallel (Fig. 2-a) and the parallel (Fig. 2-b).

Our results show that:

  1. The difference of frictional force for two boundary conditions abruptly damps with increasing distance, reflecting the fact that the two-dimensional Ising model has an only point-like critical point (Fig. 3).
  2. The frictional force itself has a singularity as a function of the temperature, which is equal to the non-equilibrium critical point investigated in Ref. [1] rather than the conventional well-known critical temperature (Fig 4).

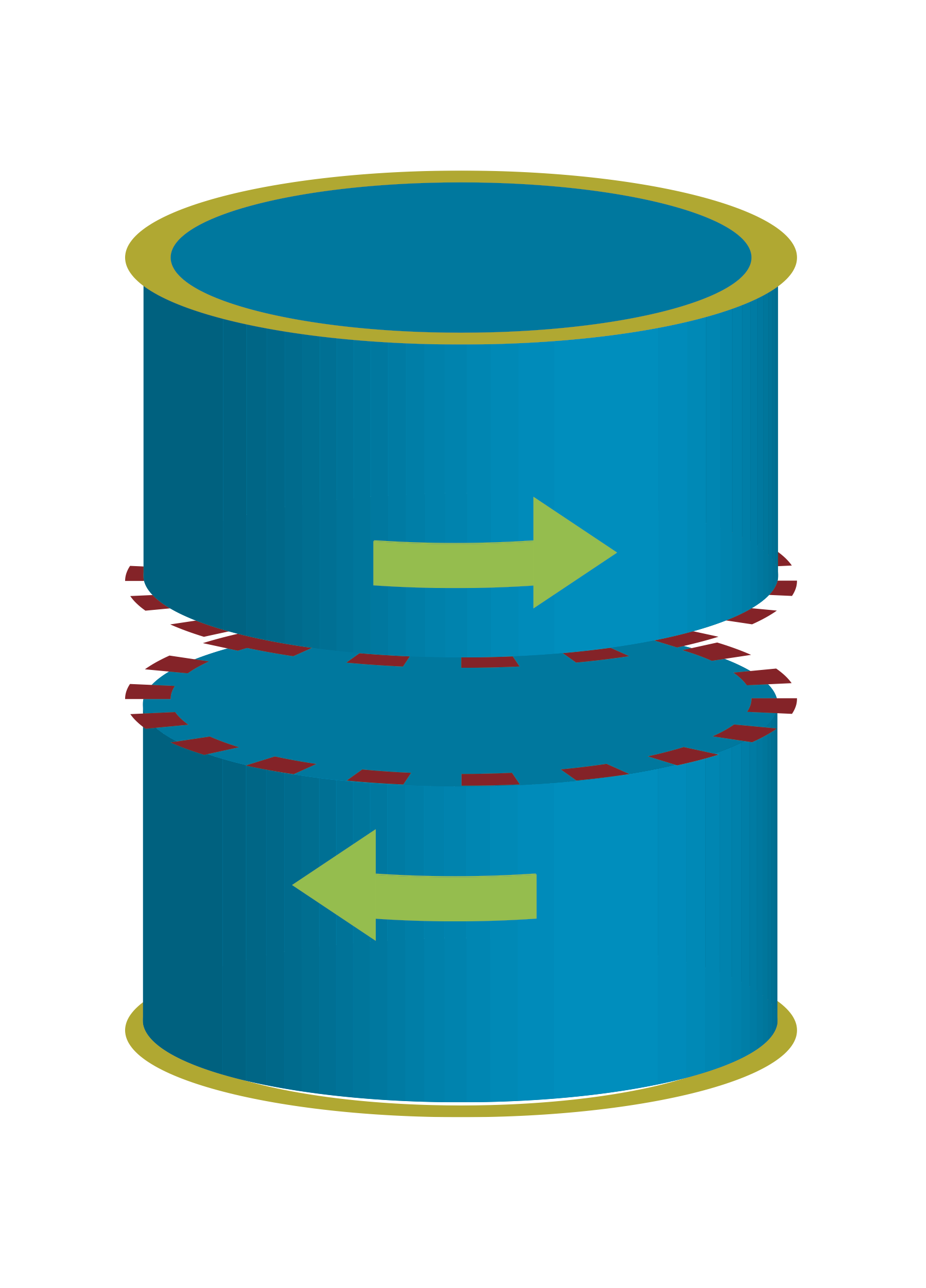
Fig. 1

Fig. 2-a

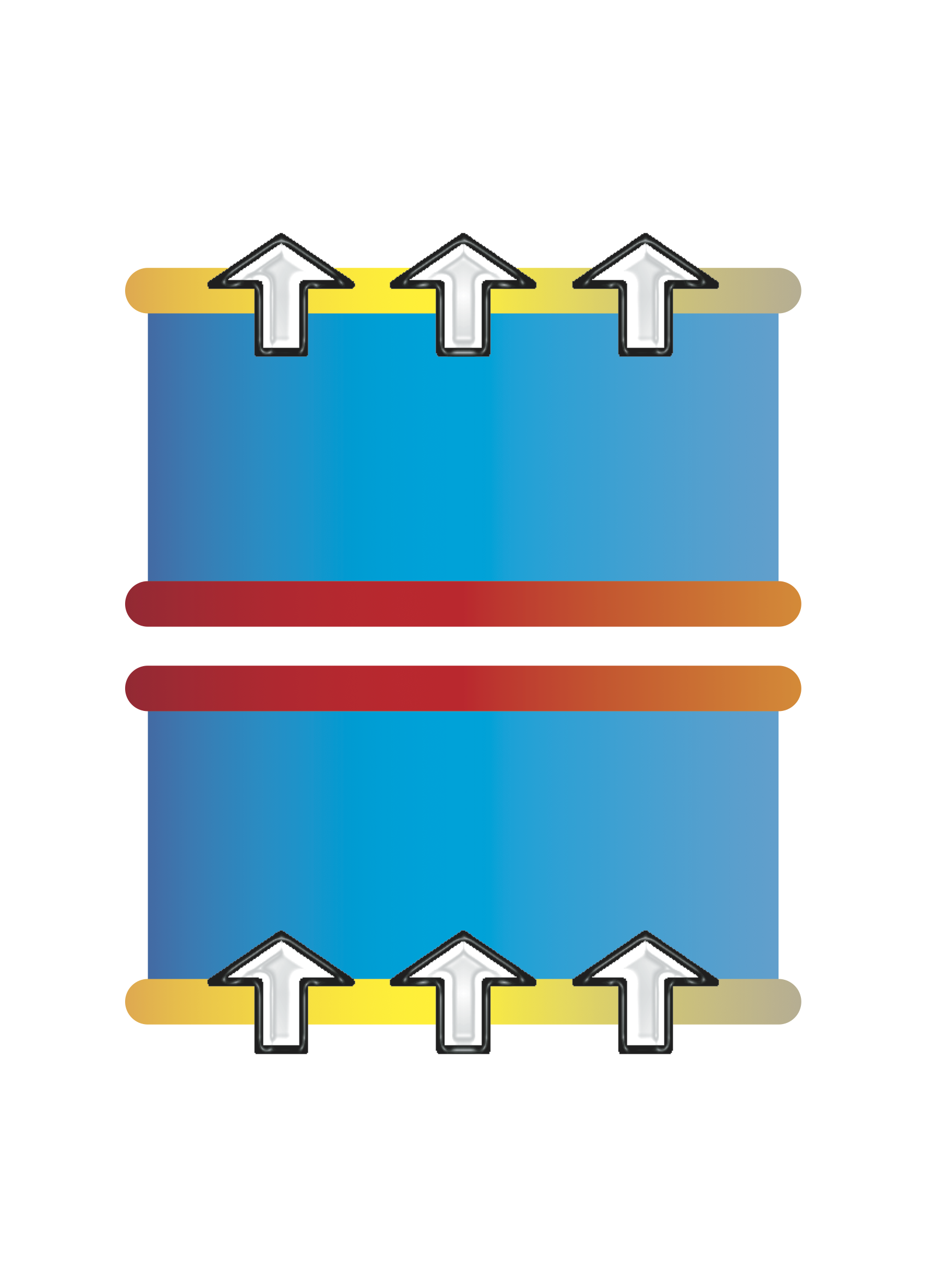
Fig. 2-b

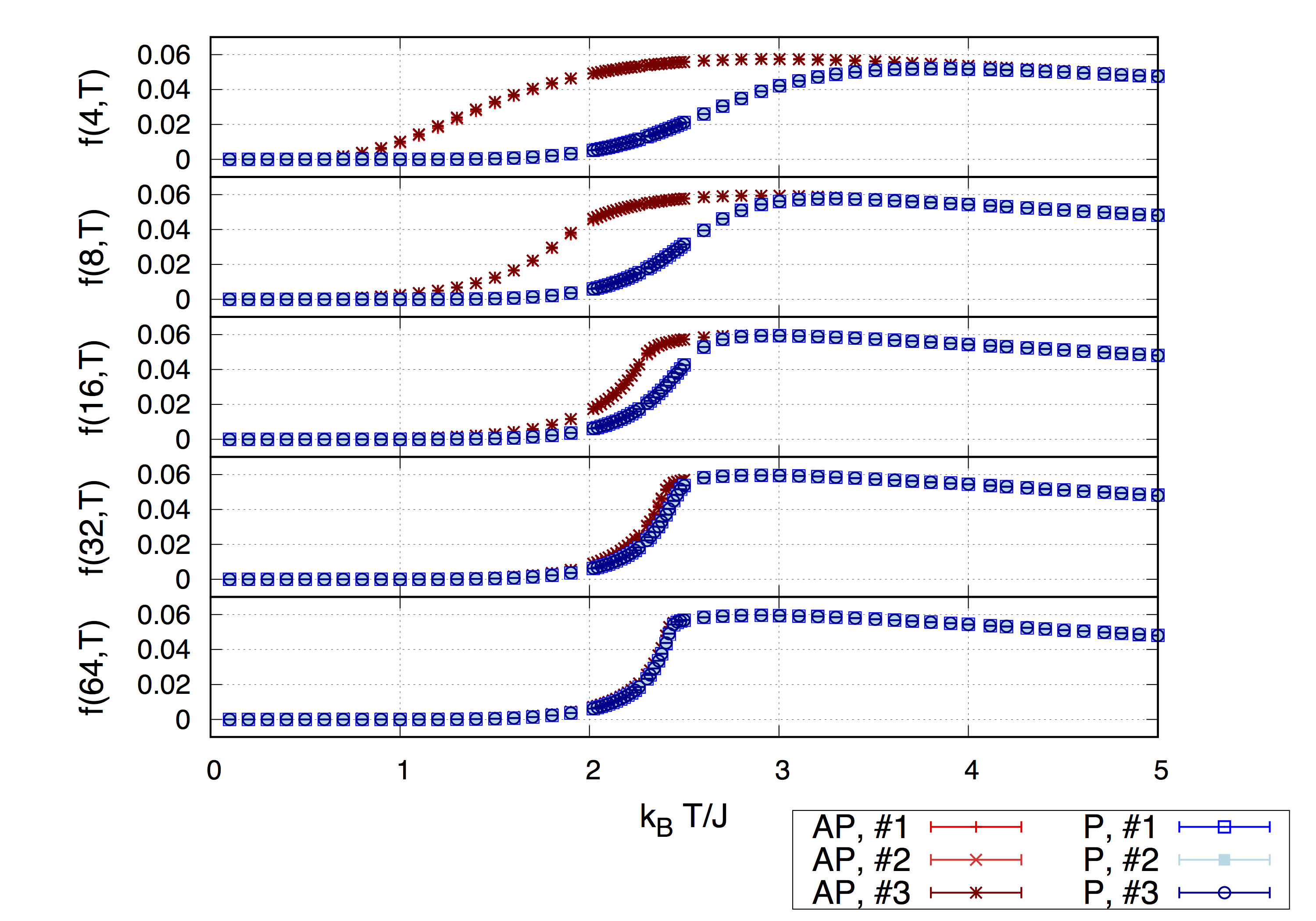
Fig. 3

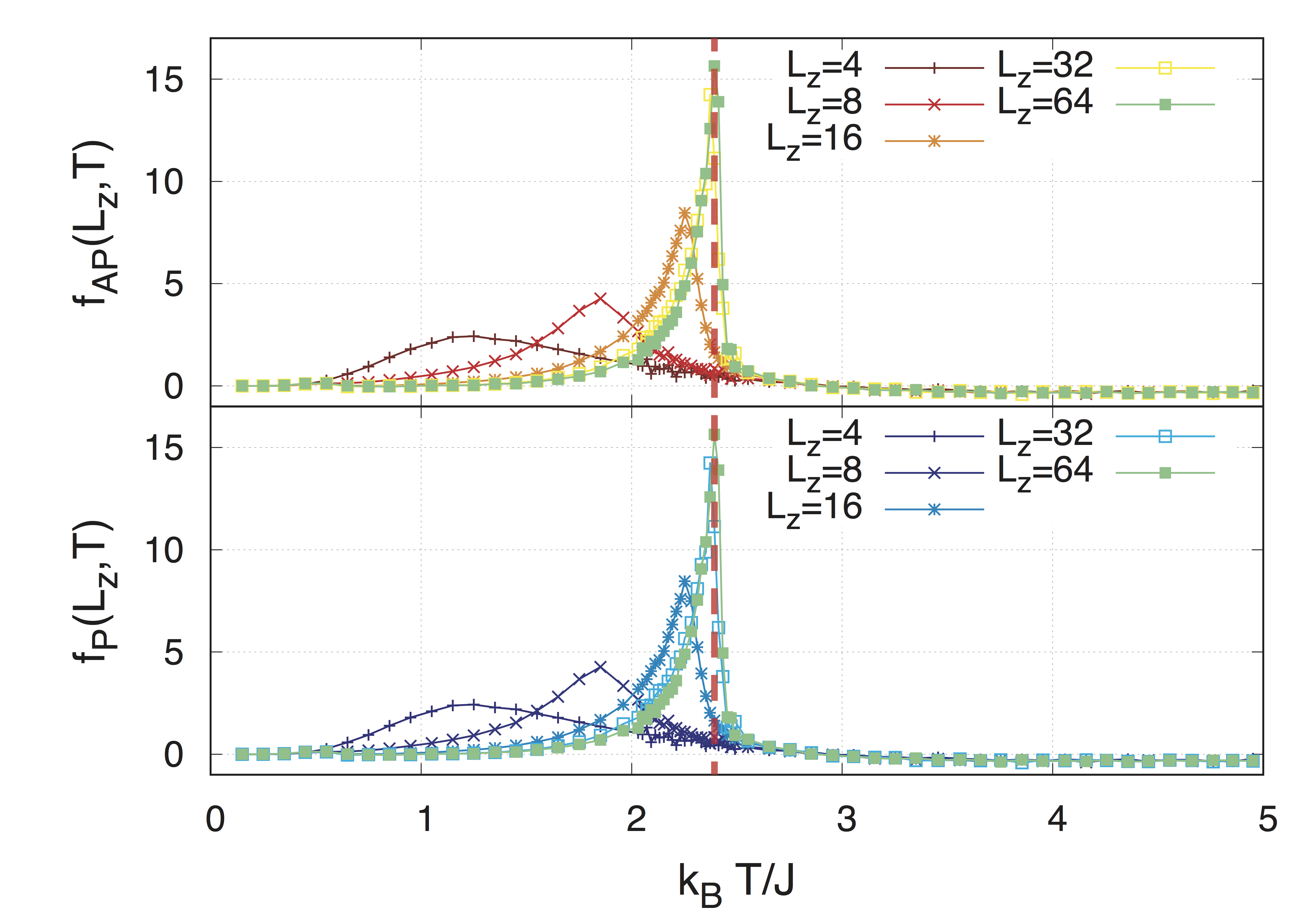
Fig. 4

References

  1. A. Hucht, Phys. Rev. E 80, 061138 (2009).

Top

Community Detection in Complex Networks (Naomichi Hatano)

The complex network refers to a class of networks that we find in various scenes of real world, including a reaction network of proteins and enzymes in a human body, an ecological network of predetors and preys, a friendship network in human societies and an airport network. It has been known that these networks have surprisingly common features, including the power-law order distribution and the small-world effect. There are many researchers going on in order to find out how this class of networks emerge and how we can characterize the generated networks. We are working particularly on the latter subject.

We have introduced the "partition function" and the "Green's function" of complex networks, referring to them the subgraph centraliry and the communicability, respectively. In particular, we showed that we can detect communities in a complex network using the communicability. For example, our analysis of the USA airport network reveals two communities of the airports on the east coast and those on the midwest and the west coast (lower-left figure) with additional two communities that bridge the former two (lower-right figure). Using this method, we can find weak and strong points of a network.

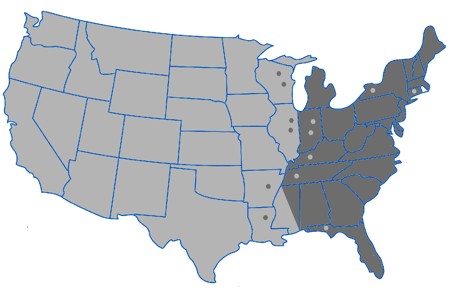
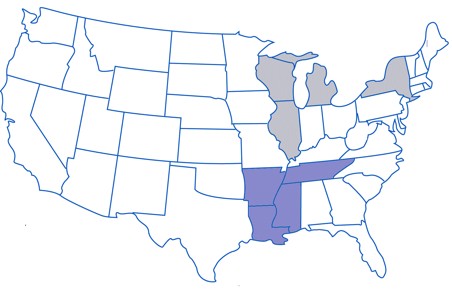
References

  1. E. Estrada, D.J. Higham and N. Hatano, Phys. Rev. E 78 (2008) 026102.
  2. E. Estrada and N. Hatano, Phys. Rev. E 77 (2008) 036111.
  3. E. Estrada and N. Hatano, Chem. Phys. Lett. 439 (2007) 247-251.

Top

Heating in integrable time-periodic systems (Takashi Ishii)

Time-periodic systems (systems under a periodically varying external field) gather attention both experimentally and theoretically because of its potential of realizing novel physical phases, such as topological phases, by using simple time-dependent Hamiltonians [1,2]. On the other hand, time-periodic systems may absorb energy from the periodic drive and the heating may break down the non-trivial quantum phases. Thus, it is an important question whether the heating occurs and to what extent the system absorbs energy from the driving.

We studied [3] the heating phenomenon in integrable time-periodic systems that can be mapped to free-fermion models.


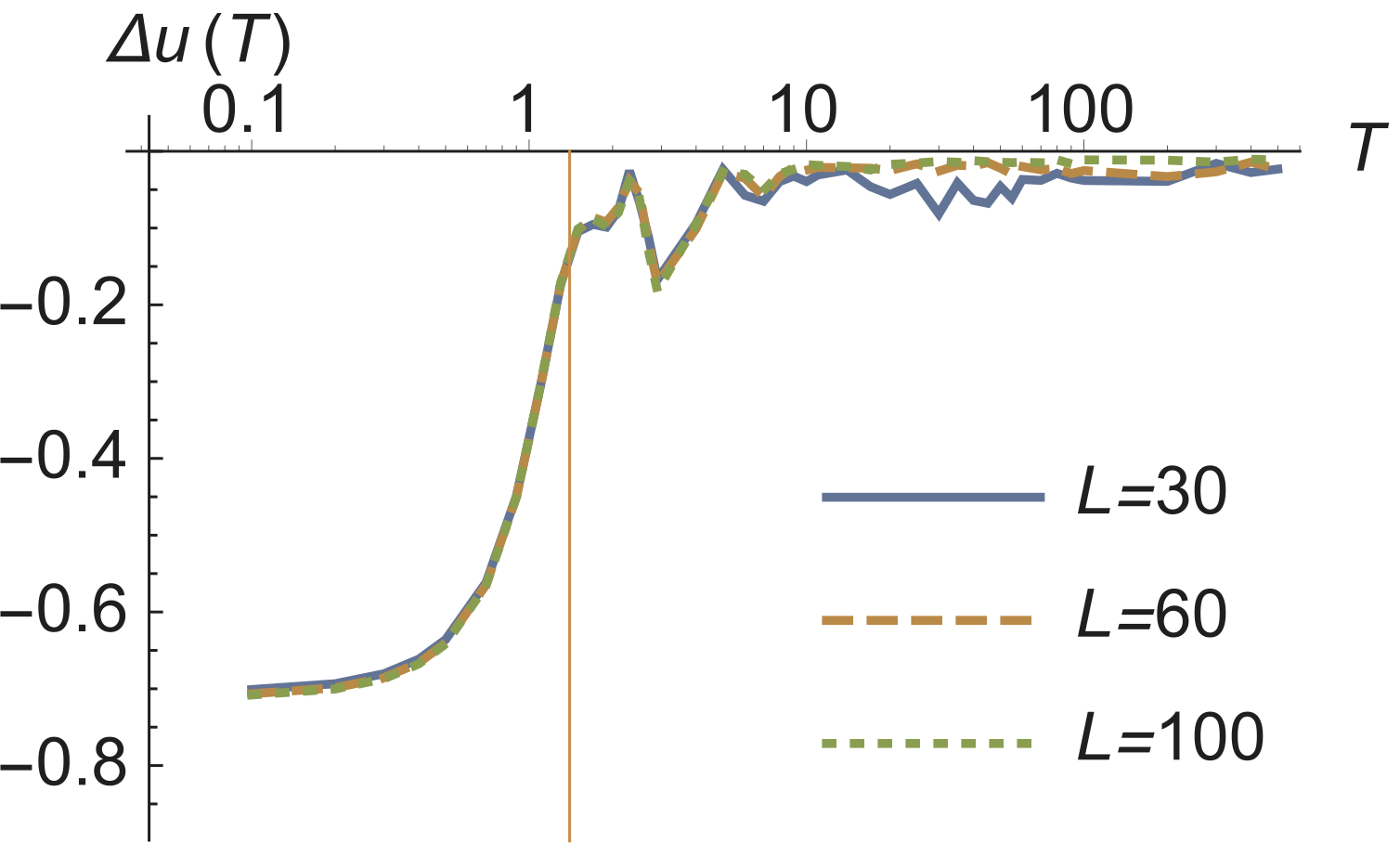
References

  1. N. Lindner, G. Rafael, and V. Galitski, Nat. Phys. 7, 490 (2011).
  2. A. G. Grushin, A. Gómez-León, and T. Neupert, PRL 112, 156801 (2014).
  3. T. Ishii, T. Kuwahara, T. Mori, and N. Hatano, PRL 120, 220602 (2018).

Top

Information Thermodynamics in Quantum Systems (Youhei Morikuni)

The paradox of Maxwell's demon is a Gedankenexperiment in which it is suggested that the second law of thermodynamics might hypothetically be violated. By applying feedback control after observing the micoroscopic state of a thermodynamic system, it appears that one could extract work beyond the limit set by the second law.

However, it has become evident through various research that the second law of thermodynamics remains valid if information obtained through measurement is also taken into account. This eventually led to the proposal of the second law of information thermodynamics as a generalization of the original statement.

Recently, Sagawa and Ueda generalized the Jarzynski relations for classical systems when measurement and feedback process is also present. We have subsequently extended the framework into quantum systems and found that similar relations hold when classical error is incorporated into projective measurements.


References

  1. Y. Morikuni and H. Tasaki, J. Stat. Phys. 143, 1 (2011).

Top

A Non-Abelian Gauge Field Theory of the Spin-Orbit Interaction and the Perfect Spin Filter (Naomichi Hatano)

The spin-orbit interaction in two-dimensional electron systems is attracting much attention because it may enable us to manipulate the electron spin with an electric field and to generate an electric current with a magnetic field. We pointed out that a non-Abelian gauge field theory (namely the Yang-Mills theory) well describes the spin-orbit interaction.

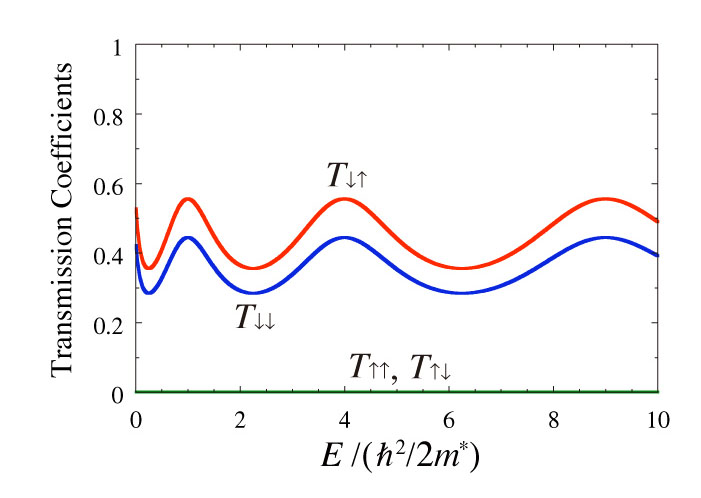
Based on it, we succeeded in proposing a perfect spin filter. The perfect spin filter is an interference circuite of an electron made with quantum wires, from which electrons of only one component of spins come out when we inject electrons with mixed spins into it. We succeeded in finding a spin filter that is perfect independent of the incident energy (figure).

References

  1. N. Hatano, R. Shirasaki and H. Nakamura, Phys. Rev. A 75 (2007) 032107.

Top

Strong Resonance of an Electromagnetic Field in a Dielectric Fractal (Naomichi Hatano)

A recent experiment observed absorption of an electromagnetic field shone on a dielectric material with a fractal structure. We proposed a theory that corresponds to the experiment and saw how an electromagnetic field behaves in a dielectric fractal, specifically in a Cantor set. We can generate a Cantor set by breaking down a line segment into three parts and removing the middle, breaking each of the remaining two parts into three and removing the middle of each, and repeating the same procedures forever. Its fractal dimentionality is 0.63. We discovered that an electromagnetic field in the Cantor set can resonate in cavities of various sizes. Depending on the frequency, the field of strength 107 times stronger than the incident field can be localized in the Cantor set (figure).

References

  1. N. Hatano, J. Phys. Soc. Jpn. 74 (2005) 3093-3111.

Top