研究室HP：http://sola.c.u-tokyo.ac.jp/

教員紹介HP：http://www.dbs.c.u-tokyo.ac.jp/labo/c_daijiro_yoshioka.html

研究テーマ：電子物性を主とした物性物理学

研究内容：

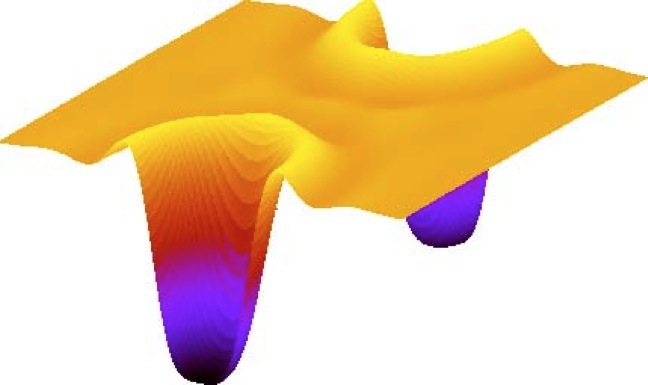
金属や半導体中の電子たちは相互作用の結果，超伝導，量子ホール効果など興味深い現象を示します．このような状態の研究をおこなっています．私たちの研究の出発点は対象となる電子系を適切に表現できるモデル・ハミルトニアンです．多電子系が相手ですから，第２量子化した形の，電子間の相互作用を含むものです．このハミルトニアンの基底状態や低エネルギーの励起状態を調べることが，研究の内容です．電子間の相互作用が含まれていますから，解析的に厳密な基底状態を求めることは普通は不可能です．そこで，主に以下の３種類の近似法で研究します．(i)平均場近似．起こっている現象の本質を表す秩序変数を推測し，それを用いた平均場近似を行う．どのような秩序変数を用いればいいのかが大問題で，それの発見が面白いところです．物理のセンスを問われます．(ii)場の理論の方法を用いた近似を行う．平均場近似と同じですが，より高精度の近似を行うことができます．計算力と長い計算を行う忍耐が必要です．(iii)小数系を計算物理の方法で攻める．有限の数の電子数のハミルトニアンは適切な基底を用いて有限次元の行列で表現できます．電子数が少なければ行列も小さくなるので，数値的に対角化して基底状態や低エネルギーの励起状態を求めることができます．最近は密度行列繰込群法(DMRG)を用いて，数十個の電子系も取り扱えるようになりました．このような計算では例えば２電子の相関関数を計算して，基底状態の性質を調べ，実現している秩序を推測することができます．そのような計算の例を図示します．ここでは分数量子ホール効果状態が見えています．このようにこの手法では量子力学の世界を絵で見ることができます．このような研究に参加して，世界中でだれも知らなかった事を初めて発見する喜びに参加しませんか．