
当研究室では物性理論、特に「物性基礎論」を中心に研究しています。我々人間のまわりを取り巻く現象には、多くの自由度がお互いに絡み合って起こるものが多々あります。そのような多自由度系を抽象化したモデルをつくり、統計力学、場の理論、計算機シミュレーションなどの手法を駆使して、現実に起こっている現象を理論的に再現してみせよう、というのが研究室の目標です。抽象化したモデルを扱うと、一見全く無関係のように見えた現象が実は共通の物理に根差していることがわかる場合がしばしばあり、それが物性基礎論の醍醐味と言えます。
最近のテーマをキーワードでまとめるとすると
非平衡統計物理学といったあたりになります。 しかし、方針としては研究固有のテーマは設定せず、新しい分野を切り拓くような研究を目標にしています。 以下に、最近の研究テーマや現在の研究テーマをいくつか具体的に紹介します。
量子統計物理学(とくに非平衡量子統計物理学)
複雑系(複雑ネットワークや経済物理学)
現在は以下のようなテーマで研究を行っています。(過去の学位論文はこちら)

量子ドットに2本の導線を接触させてできる開放量子系に対して、多電子散乱状態を厳密に構成しました。 また、左右の導線が電位差のある電子溜に繋がっている場合に、量子ドットに流れる電流(非平衡電流)を解析的に得ました。
開放量子系とは系の試料部分につながる導線などの効果により、電子の出入りが可能な量子系です。 本研究では量子ドットに2本の導線を接触させた(スピン自由度のない)系(図1)を扱いました。 重要なのは量子ドット上の電子と導線上の座標x=0の電子の間にクーロン反発があることです。
この開放型量子ドットの多電子散乱状態の厳密解を得ました。 ここで散乱状態とは自由電子平面波を入射状態とする固有状態を意味します。 この散乱状態は量子ドットでの散乱により、自由電子平面波以外に多体束縛状態が現れることが特徴的です。 例えば図1のように左側から2電子平面波を入射した場合は、2電子の座標x1、x2に対して、 |x1-x2|に関して指数関数的に減衰する2体束縛状態が現れます。
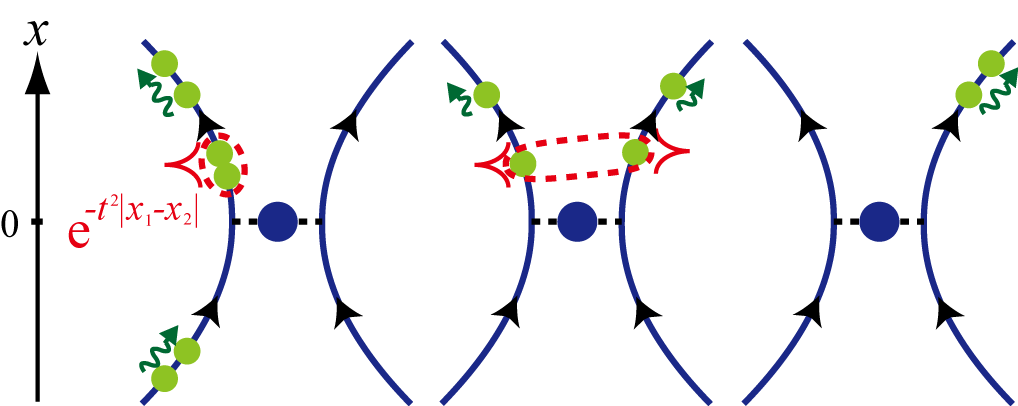
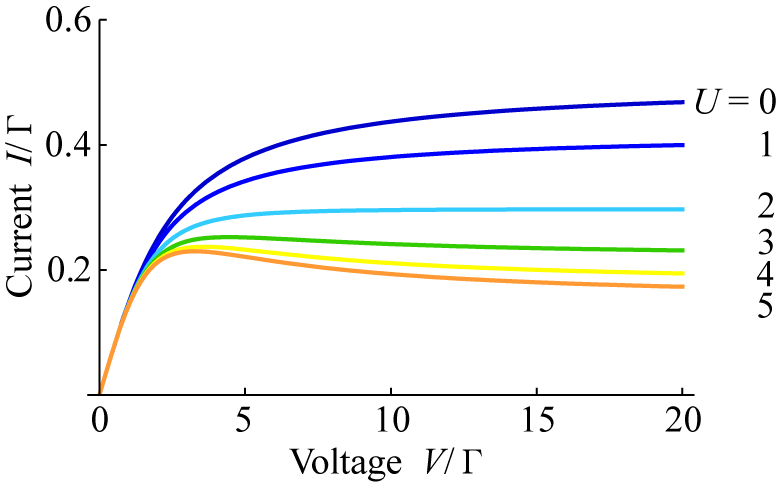
電子溜はフェルミ分布で特徴づけられるとし、電子は左右の電子溜で十分熱平衡化されてから入射されるという仮定の下で、電位差Vがある場合の電流Iを解析的に計算しました。 電流電圧特性は図2のようになります。 クーロン反発の強さUを大きくすることで電流が抑制され、さらにUを大きくすると負性の微分伝導度が現れることが分かりました。
参考文献
A. Nishino and N. Hatano, J. Phys. Soc. Jpn. 76 (2007) 063002.
A. Nishino, T. Imamura and N. Hatano, Phys. Rev. Lett. 102 (2009) 146803.

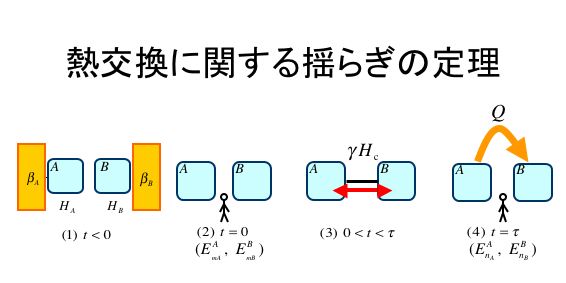
熱力学によれば、熱は必ず高温側から低温側に流れます。 しかし、系が非常に小さくなれば、熱の流れにも揺らぎが重要になってきます。 低温側から高温側へ熱が流れることも、確率的には起こりえます。 どちら向きにどのくらいの熱が流れるかを指定する確率分布を議論するのが、一般に揺らぎの定理と呼ばれている種類の理論です。
我々は、Jarezynski らが提唱した、2つの量子系の間の鉄交換に関する揺らぎの定理を再検討しました。 Jarezynski らは、2つの量子系の間の結合が弱いときには成り立つと提案していましたが、検討の結果、結合が弱いときには同時に熱も流れなくなり、無意味な定理になってしまうことを明らかにしました。 逆に、結合のハミルトニアンともともとの量子系のハミルトニアンが交換する場合には、結合がどんなに強くても定理が成り立つことを照明しました。
参考文献
S. Akagawa and N. Hatano, Prog. Theor. Phys. 121 (2009) 1157.
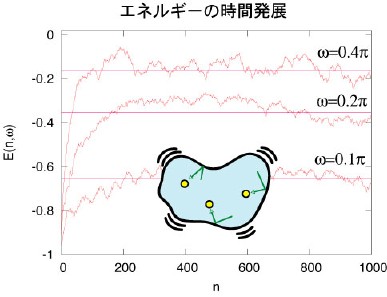
複雑に運動をする量子系を考える。単純な量子系ならば Schroedinger方程式 を直接解くことができるだろう。 また、粒子数が無限とみなせるほど大きな場合には自由度の多さを逆手にとって熱力学による記述ができる。 我々は中途半端な自由度の量子系の外場に対する応答に興味を持っている。 このような量子系は、量子ドットやナノ磁石として近年実験的にも作成されるようになった。 例えばナノスケールの小さな領域に電子をいくつか閉じ込めてその境界を外から振動させてみよう。 内部の電子のエネルギーは古典的にはどんどん上昇するが、今の場合はエネルギーはある値まで上昇すると飽和してしまうことがわかる。 我々はランダム行列を用いてこのような系のダイナミクスを調べ、飽和エネルギーと境界の振動数の関係を求めた。 つまり、境界の振動のさせ方によって電子が吸収できるエネルギーが変化する。
参考文献
M. Machida, K. Saito, and S. Miyashita: J. Phys. Soc. Jpn. 71 (2002) 2427.

量子情報科学の目標は、量子力学の重ね合わせの状態を利用して、計算や通信を行うことである。 量子的に絡み合った状態(エンタングルメントという)を用いることによって、これまで実現出来なかった速さで計算が実行できたり、誰にも破られない暗号を作ることが可能となるのだ。 したがって、量子情報科学の”資源”たるこのエンタングルメントをどのように生成するかは、非常に重要な問題である。近年、メゾスコピック系のデバイスを用いたエンタングルメント生成が活発に議論されている。
我々は、開放型量子ドットを用いたエンタングルメント生成を議論する。 図の様に導線が左右についていて真ん中に量子ドットがあるという系を考える。

2つの電子の全エネルギーは保存するが、個々の運動量は保存しないというcotunneling過程を考えると、実は導線2には、spin-singlet状態という典型的なエンタングルメントのみが透過するのである。 我々はその遷移レート(単位時間当たりどのくらい透過するかを計る量)を厳密に導出した。 これを導出するために我々はこの系の2電子散乱状態を厳密に構成した。 この厳密解は散乱状態としても興味深く新しい解である。
この図の系およびメゾスコピック系のデバイス全般に言えることは、系が開放的であるということだ。 つまり電子が導線1から流入し、導線2から出て行くので、デバイスだけでは閉じていないのだ。 このような開放系における輸送現象、およびエンタングルメント生成の理論は、今後のますます重要になるのは明らかなにもかかわらず、未だに未完成である。 我々は、この多電子の散乱状態を用いた解析が最も自然で有効なアプローチであると確信している。
本研究はまだ始まったばかりである。メゾスコピック系のエンタングルメント生成の多くの興味深い問題を解決すべく、多電子散乱状態のアプローチとその応用について現在も活発に研究中である。
参考文献
T. Imamura, A. Nishino and N. Hatano, Phys. Rev. B 80 (2009) 245323.
一般にエンタングルメントのような量子的相関は、ランダムネスが入ると壊れてゆくと考えられています。 しかし、我々はランダム磁場のある量子スピン系において、ランダム磁場を強くすると、一時的にエンタングルメントが増加する現象を発見しました。 ランダム磁場のない量子スピン系が強磁性基底状態のようにスピンが揃った状態にあると、量子性は強いもののエンタングルメントは全くありません。 そこにランダム磁場を入れると、量子性が壊される前にエンタングルメントが一時的に回復するのです。
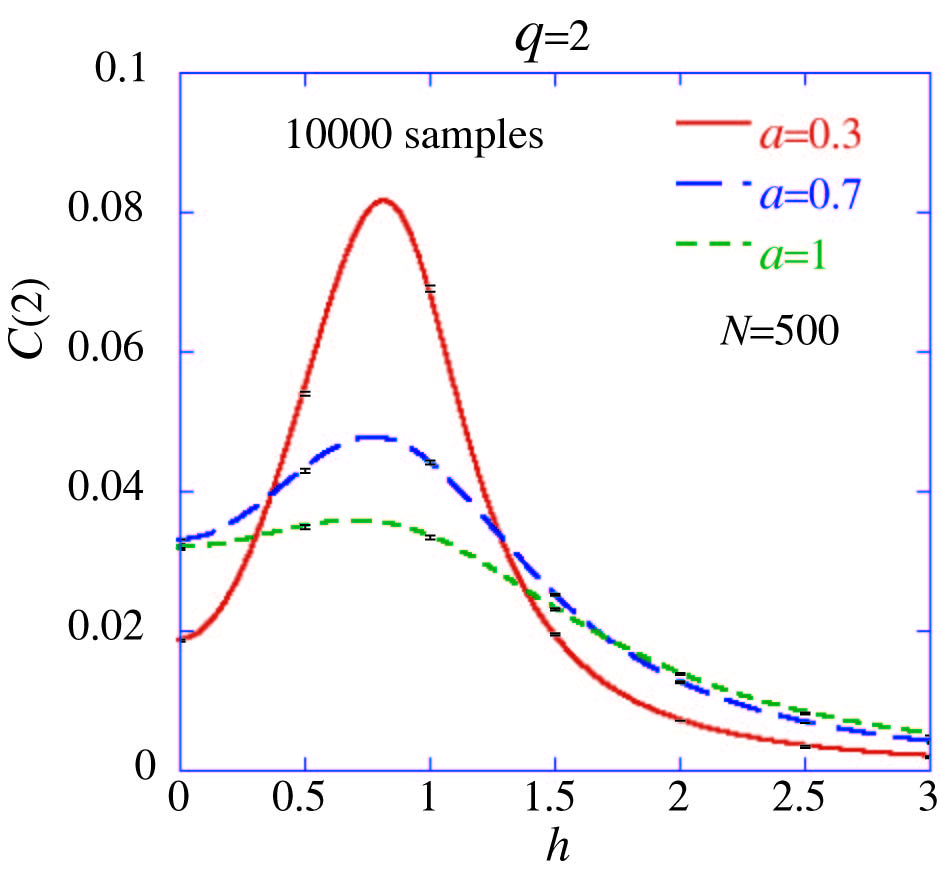
参考文献
リウビリアンとは,密度行列の運動の生成子です。 (ちょうど状態ベクトルに対するハミルトニアンと同じ関係です。) リウビリアンの固有値は,考えている系が有限次元の場合には、ハミルトニアンの固有値からすべて予測可能ですが,無限次元系の場合だと必ずしもそうではありません。 本研究では,このような予測不能な固有値を、具体的にモデルを指定して得ることを目的にしています。 この研究の背後には,全系を無限系とすると(理想化),リウビリアンの予測不能な固有値の中に複素固有値が現れ、非平衡から平衡への緩和時間に対応するのではないかという推測があります。

量子力学では、粒子がエネルギー障壁を越えて移動する「トンネル現象」が知られています。 さて、粒子がエネルギー障壁をトンネルするのにはどれくらいの時間がかかるのでしょうか。 そもそも、そんな時間は定義できるのでしょうか。

これは量子力学の基本にかかわる大問題で、昔から多くの人によって議論されてきました。 我々は最近、これに対して2つの答えを出しました。 粒子のエネルギーが、「複素エネルギー平面での分岐点」から遠ければ、「トンネリング時間」は共鳴状態の寿命の重み付き平均で定義できます。 一方、粒子のエネルギーが、「複素エネルギー平面での分岐点」に近ければ、「トンネリン時間」は定義できないことがわかりました。 前者の場合には、トンネルする粒子の確率が指数関数的に増減するので、特徴的な時間が存在するのですが、後者の場合には冪的に増減するので、特徴的な時間が定義できないのです。
参考文献量子力学的共鳴状態は、多くの量子力学の教科書では「複素固有値を 持っていると仮に理解すると便利である」という表現で現象論的に議論されています。 しかし、実際には開いた量子系に対するシュレーディンガー方程式の固有状態として正確に定義することが可能です。 その波動関数は(固有エネルギーの虚部のために)時間的に減衰しますが、(固有波数の虚部のために)空間的には遠方で発散するという形をしていま す。 一見、不思議な波動関数ですが、それに対して粒子数保存を議論することもでき(図)、数値的に正確に追跡することもできます。
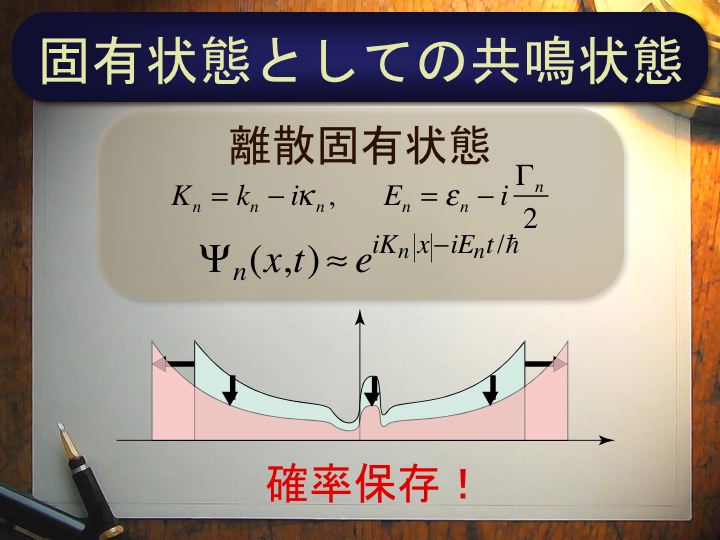
共鳴状態についての数理物理学的な理解は、まだこのような基礎的なレベルに留まっており、量子ドットにおける共鳴現象の解明と併せて、今後、大いに発展させようと考えています。
参考文献
ナノスケール・デバイスのコンダクタンスは、共鳴状態によって大きく支配されています。 共鳴状態は開放系特有の状態であり、一般に複素固有値を持つことが知られています。 この共鳴状態を算出し、ナノ領域の電子伝導を解析することが我々の研究の目的です。
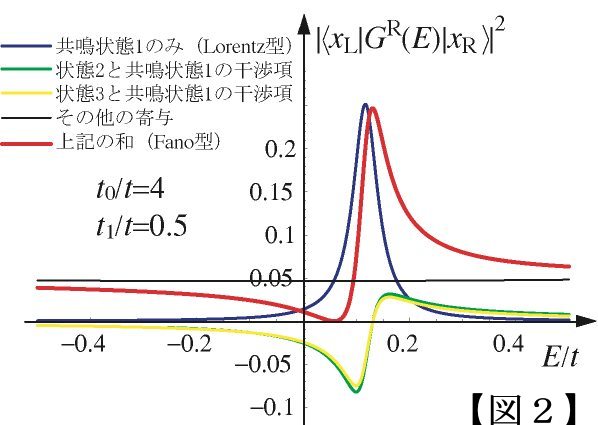
特に、2つの離散状態の間の干渉がコンダクタンスのピークの対称性を決定していることを指摘します。 非対称なコンダクタンスピークはFano共鳴と呼ばれ、1961年にU. Fanoによって研究されました [1]。 Fanoは、連続状態と離散状態の混合が、量子干渉効果によってピークの非対称性を生むと主張していました。 しかし、我々は共鳴状態を使ってグリーン関数を固有値分解することで、 Fanoピークの非対称性が離散状態の干渉項によって決定されていると主張します[2]。
ナノ領域の電気伝導は開放量子系で記述できますが、この開放量子系の理論は伝導現象を詳しく記述できるほど発達していません。 そこで、我々はこの開放性を決定している導線の効果を複素数の自己エネルギーとして表現します[3]。 すると、非エルミート性のあるハミルトニアンによって開放系を扱うことができます。 そして算出した共鳴状態を用いて、遅延グリーン関数を固有値分解することができます。 コンダクタンスは、およそグリーン関数の絶対値の2乗であり、このとき干渉項が現れます。 干渉項がコンダクタンスのピークに非対称性を生じさせることを示すことができます。 つまり、Fano共鳴は離散状態の間の結合によって生じると言えます。
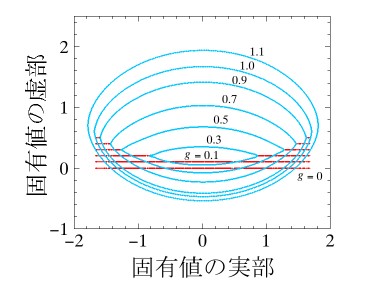
例として、単純なABリング【図1】を考えます。この系の固有状態を複素エネルギー平面上に図示しました。 導線とドットの間のホッピングエネルギーを摂動として増加させたときの共鳴固有値の流れを示しています。 t1=0の時、サイト0に局在する状態は実数エネルギーを持つ固有状態ですが、ホッピングエネルギーを増加させると、 固有値が複素数平面に移動して共鳴状態となります。このとき、コンダクタンスは【図2】に見られるように、 他の束縛状態との干渉項が生じることでFanoコンダクタンスを形成します。このような観点からFano共鳴は特異な量子干渉効果ではなく、 一般的な伝導現象の一例であると言えます。現在、この非エルミート性のあるハミルトニアンから、 存知の様々な伝導現象を解析することまたは未知の現象を予想することを研究しています。
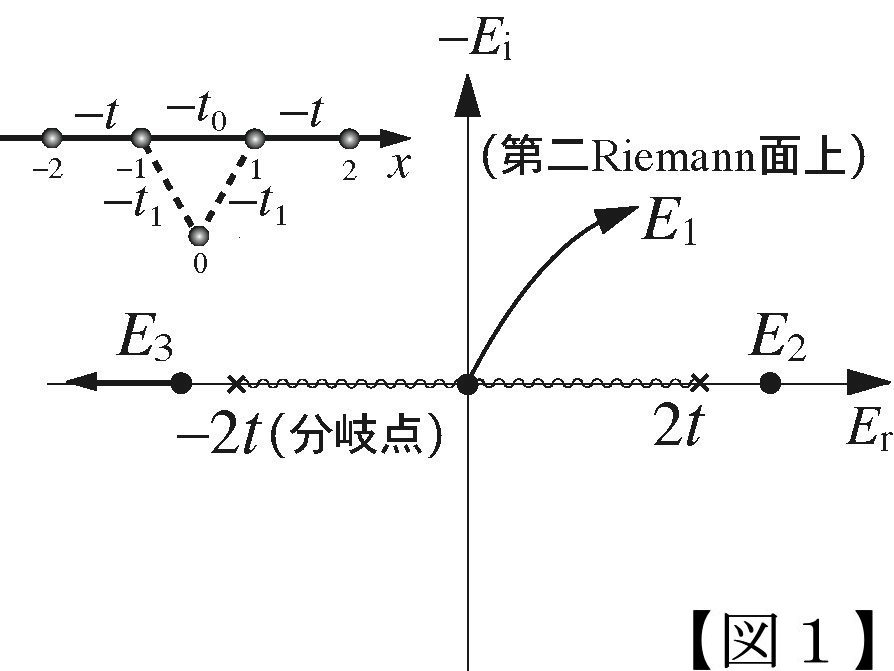
参考文献
[1] U. Fano, Phys. Rev. 124 (1961) 1866.
[2] K. Sasada, N. Hatano, Physica E 29 (2005) 609.
[3] S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, 1995

光格子中の希薄なBose気体の基底状態における超流動-Mott絶縁体相転移はBose-Hubbard modelを用いて記述できることがわかっています。 光格子とは同軸上で向かい合わせにレーザーを照射させたときにできる周期的な定在波のことで、Bose粒子のトラップとして用いることができます。 レーザーの強度を制御することにより このトラップの深さを変化させることができ、これによって相転移が起きます。 また、近年では2種類のBose粒子を混合させたBose-Bose混合系における超流動-Mott絶縁体相転移も理論実験両面から研究されています。 本研究では外部トラップポテンシャルがない一様系、調和ポテンシャルを外部トラップポテンシャルとして加えた非一様系で、 Gutzwiller近似という方法で超流動オーダーパラメーターという秩序変数を計算することによって超流動-Mott絶縁体相転移の相図(既知)を再現し(下図)、 Bose-Bose混合系の一様系においても同じ方法を用いてこの相転移の相図を計算しました。


1995年にアルカリ原子を用いたBose-Einstein凝縮が実現されて以来、 極低温における中性原子系の研究は急速な発展を遂げています。 我々は、光格子と呼ばれる、レーザーの干渉を用いて作った周期ポテンシャル中に Bose-Einstein凝縮体を閉じ込めた時に起こる物理現象に興味 を持って研究を行っています。 Bose-Einstein凝縮体の振る舞いは、Gross-Petaevskii方程式と呼ばれる非線形 Shrodinger方程式によって記述されますが、 Bose-Einstein凝縮体が光格子中において、周期ポテンシャルと非線形性に起因する興味 深い性質を示すことが理論、 実験の両面でわかってきました。最近、我々はBose-Einstein凝縮体を光格子中で加速し、 凝縮体が異なるエネルギーバンド間をトンネルする際の非線形性の効果(下図)について研究を行っています。
金属中の不純物を徐々に増やしていくと、ある濃度に達したところで絶縁体になります。 これは、水面の波が杭に散乱されて前へ進めなくなるのと同じように、電子波が不純物に散乱されて伝導できなくなるからです。 この現象を「アンダーソン局在」といいます。電子波が「局在」(空間的に広がっていけない状態のこと)するかどうかは、 不純物濃度と電子波のエネルギーに依ります。 また、局在している場合にも、どれくらい強く局在しているかを知る必要があります。
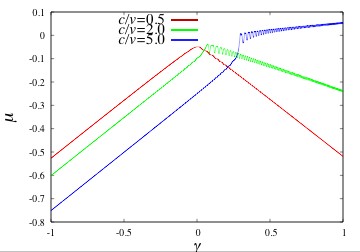
これらのことを知るために、新しいモデル(一部で Hatano-Nelson モデルと呼ばれる)を提唱しました。 このモデルでは、不純物を含んだ金属のモデルに、本来物理的にはあり得ない「虚数ベクトルポテンシャル」を導入して、 ハミルトニアンを非エルミートにします。故意に非エルミートにしたハミルトニアンの複素固有値(下図)を調べると、 本来知りたかった電子の局在状態の様子を知ることができるのです。
参考文献
N. Hatano and D.R. Nelson, Phys. Rev. Lett. 77 (1996) 570-573.

ハミルトニアンの運動量演算子に複素ベクトルポテンシャルを付加した、非エルミートなハミルトニアンを導入します。
その非エルミートなハミルトニアンのエネルギー固有値の構造から、エルミート模型の相関長が算出できることを、
いくつかの強相関量子系で見い出しました。例えば,ハーフフィルドのハバード模型を非エルミート化すると,
モット絶縁体(下図を参照)の相関長が求まります。
この非エルミート化の操作は,複素運動量空間内をスキャンする操作に対応します。
通常のエルミート模型の解析では、運動量空間の実軸上での情報しか得られませんが、
我々の非エルミート化により複素運動量空間内に侵入することができます。
我々の研究を通じ,複素運動量空間内には、エルミート模型の相関長の情報が含まれていることが分かってきました。
参考文献
Y. Nakamura and N. Hatano, J. Phys. Soc. Jpn. 75 (2006) 104001.
「複雑ネットワーク」とは、例えば人体中のタンパク質と酵素の反応のネットワーク、生態系における捕食者・被捕食者のネットワーク、あるいは社会における交友関係のネットワークや、空港間のフライトのネットワークなどの総称で、これら様々な場面で現れるネットワークが、驚くべきことにいくつかの共通の性質を持っていることがわかってきました。 現在、そのようなネットワークがどのように生成されるか、そしてできあがったネットワークをどのように定量的に特徴付けるかという2つの側面から盛んに研究が行われています。 我々のグループでは、特に後者の立場から複雑ネットワークを研究しています。
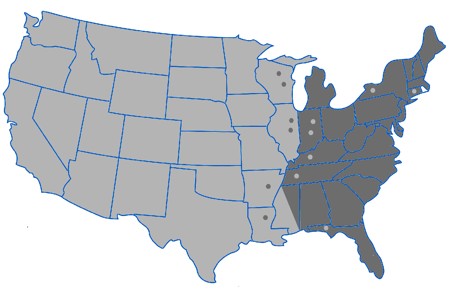
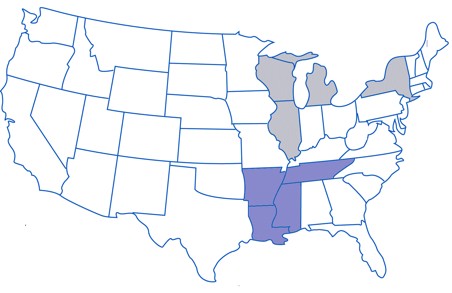
我々は複雑ネットワークの「分配関数」や「グリーン関数」と呼ぶべき量を定義し、それぞれの意味を考慮して Subgraph centraliry, Communicability と名付けました。 特に Communicability を使うと、複雑ネットワークの中にどのようなコミュニティーが存在するかを検出することができます。 例えば、アメリカの空港のネットワークを解析したところ、東海岸の空港と、中西部の空港の2つのコミュニティーが存在すること(左下図)、そして、それらを橋渡しするコミュニティーが2つ存在すること(右下図)を明らかにしました。 この方法を使うと、そのネットワークにどのような弱点があるかなどを調べることができます。
参考文献
E. Estrada, D.J. Higham and N. Hatano, Phys. Rev. E 78 (2008) 026102.
E. Estrada and N. Hatano, Phys. Rev. E 77 (2008) 036111.
E. Estrada and N. Hatano, Chem. Phys. Lett. 439 (2007) 247--251.
囚人のジレンマがある状況で、ネットワーク上のゲームを考えました。 空間的な構造が無い時には非協力的な行動が支配的になりますが、ネットワークという空間的な構造がある場合には協力行動が生まれやすくなることが知られています。 そこで我々は具体的にそのネットワークが協力行動を促進する条件を、制度の用意平均場金治を使って導きました。
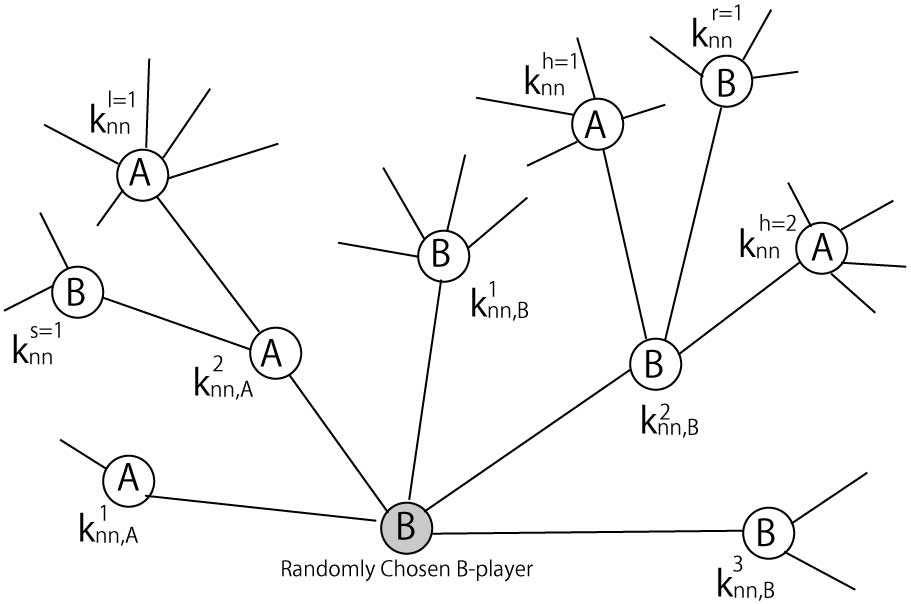
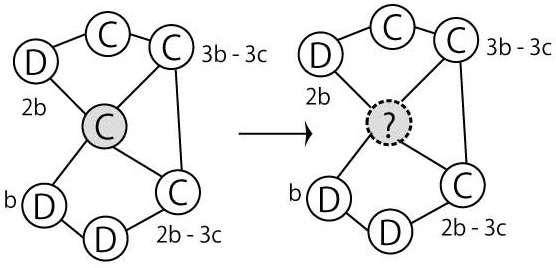
「複雑ネットワーク」の時間発展モデルの1つに適応度モデルがあります。これは、ノードの次数と適応度が大きいほど、そのノードの次数が成長しやすいというモデルです。適応度は何かしらの分布に従った値をとり各ノードに与えられるのですが、我々はとあるノードにのみ恣意的な適応度を与えるという特別な扱いをし、そのノードの次数の時間発展を議論しました。
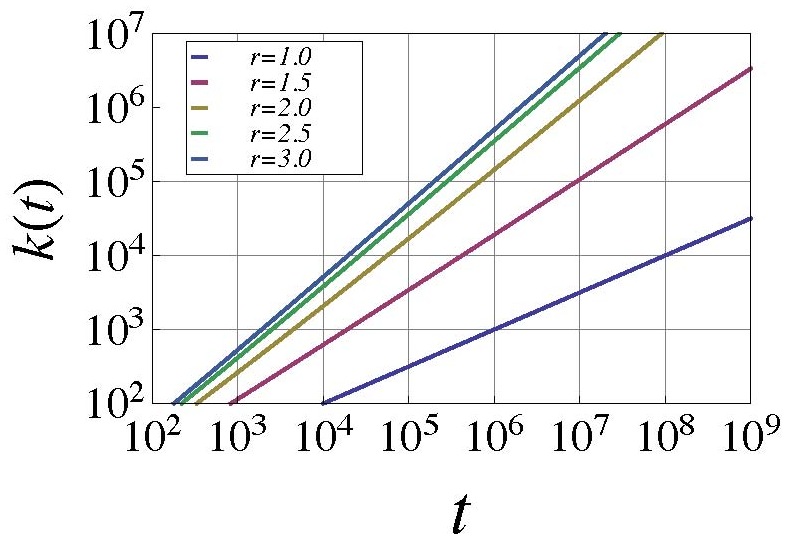
その結果、ある一定以上の適応度を与えても、次数の時間発展のべき指数が変化しない事を明らかにしました。下図は特別視したノードの次数をk(t)、適応度をr、時刻をtとしてk(t)の微分方程式を解き、両対数プロットした図です。このグラフからrが2以上ではべき指数が変化しない事がわかります。

近年、統計力学の観点から、経済・金融現象を研究する動きが国内外で盛んになってきている。 この背景には以下のような期待がある。統計物理では、個々の要素(原子や分子など)の性質がわかっていても、 それらが多数集まって系(磁石や細胞など)をなすと、個々の性質からは直接想像できない新たな現象や機能が発現する。 この統計物理における最も興味深い部分が、そのまま経済・金融現象にもあてはまるのではないかという期待である。
例えば、個々の投資家が利益を追求するという行動の特性がわかっていても、 その結果として発現する株価や為替の変動にベキ的なゆらぎが現れる現象を、単純には説明することができない。 しかし、統計力学的な観点から、ミクロな要素間(ここでは投資家間)の相互作用を規定したモデルを構築することにより、 価格変動や所得分布のベキ的な振舞を再現できることがわかってきた。 つまり、ミクロとマクロをつなぐ統計力学の手法が、金融・経済現象の理解に大いに役立つと期待されるのである。
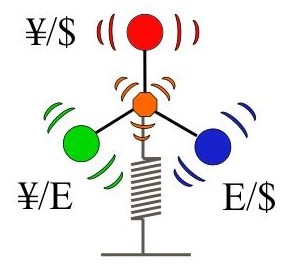
我々は、特に複数の為替相場のゆらぎと相互作用に着目して研究をおこなっている。 円ドル、ドルユーロ、円ユーロレートをそれぞれ一次元ランダムウォーカーとしてとらえると、 それらの重心に復元力が働いているという理解ができることなどが わかってきている。(下図)
参考文献
Y. Aiba and N. Hatano, Physica A 371 (2006) 572.
Y. Aiba and N. Hatano, Physica A 344 (2004) 174--177.
Y. Aiba, N. Hatano and H. Takayasu, Physica A 324 (2003) 253--257.
Y. Aiba, N. Hatano, H. Takayasu, et al: Physica A 310 (2002) 467.
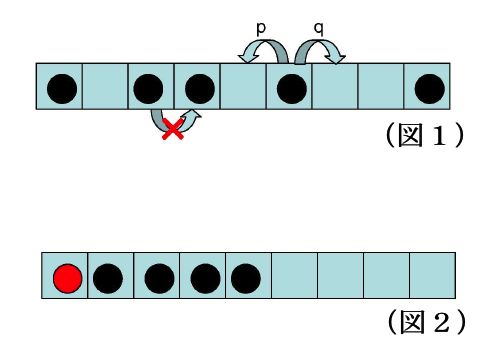
非対称単純排他過程(Asymmetric Simple Exclusion Process, ASEP)とは、 確率的な時間発展をする古典的な粒子系であり、ルールは以下の2つからなる。(図1) 1.各粒子は左隣へレートpで右隣へレートqでホップする。(非対称な拡散の効果) 2.ただし隣のサイトが他の粒子によって占有されている場合は粒子はホップできないとする。 (排他効果を介した粒子間相互作用の効果)
この拡散と相互作用の効果が競合して、ASEPは非平衡定常状態における相転移やキンクの存在など興味深い物理現象を引き起こす。 さらに、この模型は可積分な数理構造を持ち、これらの現象を厳密に解析することが出来る。
我々は、図2のような階段型の初期条件で、かつ粒子が右にしか行かない場合(図1でp=0の場合)に、 ある一つ粒子(図2では赤い粒子)に着目してそれがどのように時間発展するか、特にその長時間での振る舞いを考察した。 もし上のルール2がなければ粒子は長時間極限において単純なブラウン運動する。 一方ASEPの場合は粒子間相互作用によって、この粒子の運動は単純なブラウン運動ではなく、 エルミートランダム行列の最大固有値の運動と等しいことを明らかにした。
参考文献
T. Imamura and T. Sasamoto, J. Stat. Phys. 128 (2007) 799.
ランダム行列理論は行列要素が乱数の行列のことであり、 量子カオスの準位統計やメゾスコピック系の輸送現象等物理学の様々な分野で応用されている。 最近ランダム行列理論と非平衡統計物理学との新たなつながりが見出され注目されている。 非平衡統計物理学の重要な普遍クラスである、一次元Kardar-Parisi-Zhang(KPZ)クラスに属する様々な確率モデルにおいて、 物理量のゆらぎの分布関数が厳密に解析され、ランダム行列理論の最大固有値分布(Tracy-Widom分布)と等しいことが明らかにされたのである。
その代表的な確率モデルとして、一次元多核成長模型がある。 そのルールは【図1】で示されている。 時刻t=0で高さ1の核が生成する(【図1】(i))。 核は時間とともに一定速度で左右に成長し1層目を形成する。 その後1層目の上に核が確率的に生成し、 これらの核も一旦生成すると左右に一定速度で成長し2層目以降を形成する(【図1】(ii))。 左右への核の成長によって、2つの核が衝突する場合があるがその時は合体して一つの層を形成する(【図1】(iii)の2層目)。
我々はこの多核成長模型の高さゆらぎの解析を行っている。 【図2】のように、半無限系において、高さゆらぎの分布関数は原点からバルクに遠ざかるにつれて GSE(Gaussian Symplectic Ensemble)から GUE(Gaussian Unitary Ensemble)のTracy-Widom分布へ遷移することが分かった。
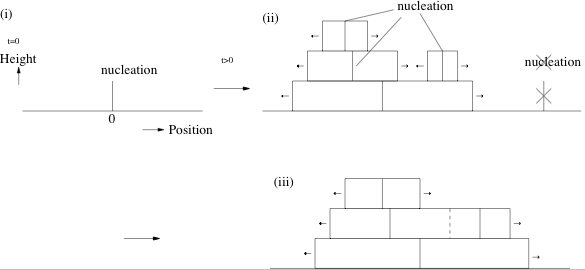 【図1】
【図1】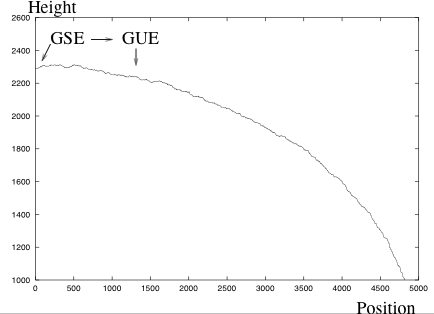 【図2】
【図2】
参考文献
T. Imamura and T. Sasamoto, Phys. Rev. E 71 (2005) 041606.
T. Imamura and T. Sasamoto, Nucl. Phys. B 699 (2004) 503.
T. Sasamoto and T. Imamura, J. Stat. Phys. 115 (2004) 749-803.

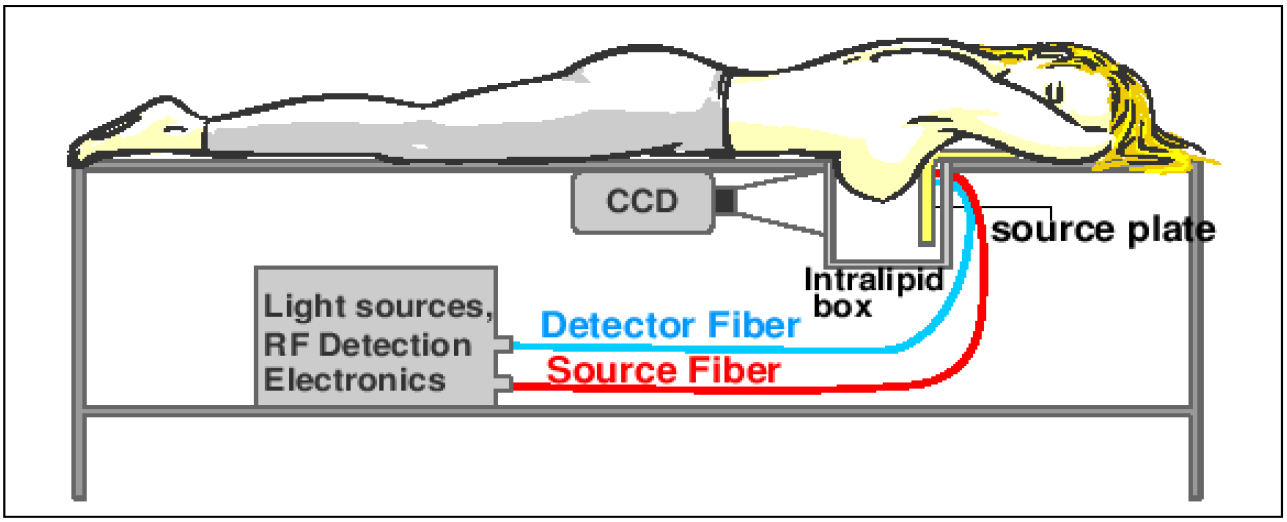
放射輸送方程式(Radiative Transport Equation)はボルツマン方程式の一種で、 チャンドラセカールによって導入されて以来 [1]、生物組織のトモグラフィーや 宇宙物理、地球物理(大気や海洋)、原子炉内の中性子の輸送現象など、 様々な分野で使われています。3次元の放射輸送方程式を解くことは難しく、 近似により拡散方程式に落とすことがしばしば行われます (吸収係数が小さく、かつソースから離れているときに良い近似にな る)。
我々は、3次元の放射輸送方程式と拡散方程式との関係について調べました [2,3]。 その結果、どんなにソースから離れていても二つの方程式から計算される エネルギー密度は完全には一致しないことを発見しました [4]。
伝統的に、拡散方程式を導くときにしばしば弾道項が導入されます [5]。 我々はさらに、この弾道項の導入が近似を悪くすることを示しました。 つまり、 正しい拡散近似は弾道項を導入することなくなされるべきであることがわかりました。
図は、ペンシルバニア大学医学部で2007年に実現された、 拡散方程式による光トモグラフィーの概念図(http://www.mmrrcc.upenn.edu/)。
参考文献
[1] S. Chandrasekhar, Radiative Transfer(Dover, New York, 1960)
[2] M. Machida, G.Y. Panasyuk, J. C. Schotland and V. A. Markel, J. Phys. A: Math. Theor. 43 (2010) 065402.
[2] M. Machida, G.Y. Panasyuk, J. C. Schotland and V. A. Markel, J. Opt. Soc. Am. A 26 (2009) 1291. (Virtual Journal for Biomedical Optics)
[3] これは、例えば相対論とニュートン力学とがパラメータ βによって連続的につながっていることとは決定的に異なります。
[4] A. Ishimaru, Wave Propagation and Scattering in Random Media(Academic Press, San Diego, 1978)
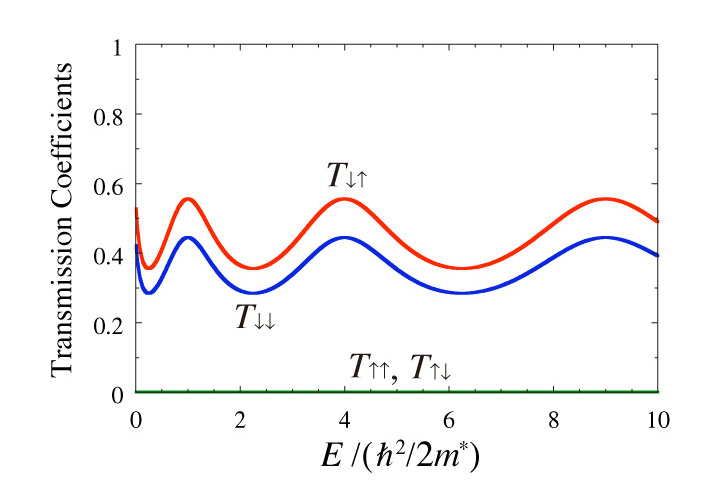
2次元電子系で発生するスピン軌道相互作用は、電場で電子のスピンを 操作したり、磁場で電流を発生させたりできる可能性が指摘されて、 注目されています。我々は、量子細線でのスピン軌道相互作用に着目して研究を進めています。新しい成果として、 スピン軌道相互作用を非可換 ゲージ場理論(Yang-Mills理論)で扱えることを指摘しました。 その理解を基にして、完全スピンフィルターを構成することに成功しました。 完全スピンフィルターとは、量子細線を使った電子の干渉路で、一方か らスピンが混合した電子群を入射しても、 もう一方から下向きのスピン しか出てこないような回路です。 我々は、どのような入射エネルギーでも完全であるスピンフィルターの構成に成功しました(図)。
参考文献
N. Hatano, R. Shirasaki and H. Nakamura, Phys. Rev. A 75 (2007) 032107.
通常、超伝導体の渦は単位磁束量子と呼ばれる最小単位の磁束を持つとされています。 産業総合研究所の田中康資、イリノイ大(当時)のE. Bavaev、および我々はそれぞれ独立に、 MgB2などで知られているようにフェルミ面が2枚存在するためギャップ関数が2種類あらわれるような超伝導体(2-ギャップ超伝導体)では2種類の渦が存在し、2種の渦の束縛状態は単位磁束量子を持つ通常の渦となるが、束縛が解けるとそれぞれの渦に単位磁束量子が分割されることを指摘しました。 すなわち、磁束の最小単位と思われていた単位磁束量子よりもさらに小さい磁束を持った渦が存在することを意味します。 さらに我々は、束縛が解けた状態が熱力学的に安定に存在し得ることを示しました。 薄膜系でこのような特異な渦状態が発生し得る事が予測されます。
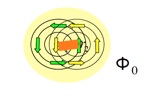
【図1】2種の渦の束縛状態。単位磁束量子を持った通常の渦となっています。
【図2】2種の渦が引き離された状態。それぞれの渦に単位磁束量子が分割されていて、その比は2つのギャップ関数の振幅の比の2乗で与えられます。
2-ギャップ間の相対位相による内的ジョセフソン相互作用の効果により、2種の渦の間にはギャップ関数の位相のとびをあらわすストリングが走ります。
表題論文では、ストリングのエントロピー利得の効果により超伝導転移温度近傍(超伝導相のなかの高温領域)でストリングによる束縛が解けた状態が安定化される事を示しました。
 【図2】
【図2】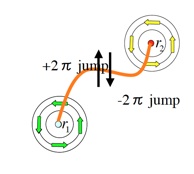
参考文献
J. Goryo, S. Soma, and H. Matsukawa, Europhysics Letters 80 (2007) 17002.
Kerr効果は光の反射の際に偏光面が回転する現象であり、磁性体など時間反転対称性の破れがある系で生じます。 最近Sr2RuO4という物質の超伝導状態でKerr効果が観測されました、 そのため、この超伝導状態は時間反転対称性を自発的に破るカイラルp-波状態である可能性が非常に高いと考えられています。 こうした状況の中、私はカイラルp-波状態のKerr効果の起源には時間反転の破れと同時に不純物効果も本質的な働きをしている事を最初に指摘しました。
参考文献
Jun Goryo, Phys. Rev. B 78 (2008) 060501(R). (Editor's Suggestion)
最近2次元の電子系で量子スピンホール効果が盛んに議論されています。 量子スピンホール効果は電場に対して垂直な方向にスピン流が発生し、その伝導度が量子化される現象です。 量子スピンホール系には一般に、ラシュバ項とよばれる上向きスピンと下向きスピンの電子を結合させるような相互作用が存在し、2次元面に垂直な電場で調節できます。 そこで我々は、電子間クーロン相互作用もとりこんだ量子スピンホール系の電磁気応答について詳細に調べました。 その結果、ラシュバ結合と電子相関の強さが適当な領域にあるとき、スピンホール伝導度の2次の効果でロンドン方程式が得られる事を示しました。 ロンドン方程式は超伝導体のマイスナー効果を記述する方程式であり、この方程式が量子スピンホール系にも現われる点が興味深いです。
参考文献
Jun Goryo, and Nobuki Maeda,“The London equation in the quantum spin Hall system with an
electronic correlation”(投稿中)
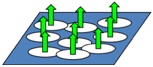
周期ポテンシャル下の2次元電子系の量子ホール効果を考えます。 量子力学の非断熱効果を考慮することにより、伝導度が非常に短い時間スケール(ピコ秒ないしナノ秒)で時間変動していることを見出しました。
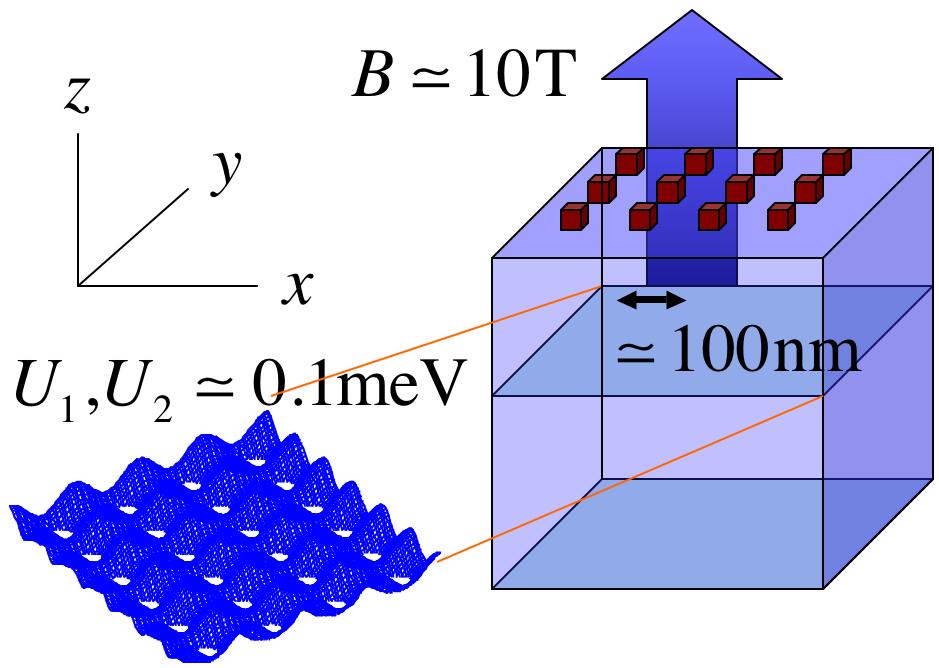
【図1】にあるように、z軸方向に磁場のかかった半導体中の超格子構造を考えます。
y軸方向の電場に対してx軸方向の電流を考えると、
このx軸方向の伝導度がe2/hの整数倍になることが知られています(整数量子ホール効果)。
従来、伝導度は理論的には断熱近似を用いて計算されていました。
これに非断熱の効果を考慮することにより、伝導度がピコ秒からナノ秒のオーダーで量子ゆらぎによって時間変動していることがわかりました。
式の上では、振動の周期はフェルミエネルギーの上下にある2準位間のギャップに反比例します。
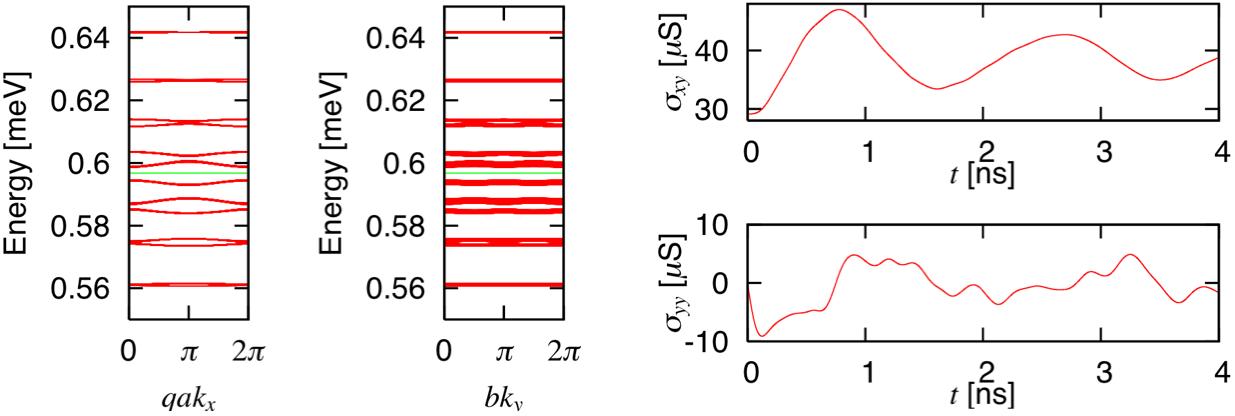
【図2】(右) は、【図1】の系における伝導度の時間依存性を、数値計算によって実際に求めたものです。
【図2】(左) は系のバンド構造です。緑の線はフェルミエネルギーを示しています。
 【図1】
【図1】
 【図2】
【図2】
参考文献
M. Machida, J. Goryo, and N. Hatano, J. Phys. Soc. Jpn. 77 (2008) 024713.
M. Machida, N. Hatano, and J. Goryo, J. Phys. Soc. Jpn. 75 (2006) 063704.
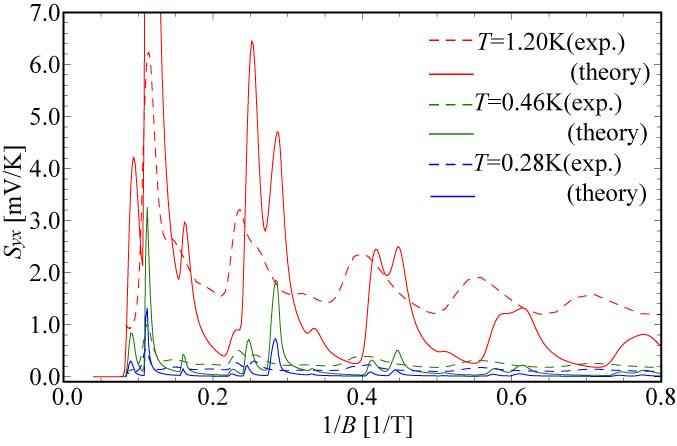
極低温における熱輸送現象について研究しています。磁場をz方向に熱流をx方向にかけたとき、互いに垂直な y方向に熱流が流れる現象をネルンスト効果(Nernst-Ettingshausen effect)といいます。 2005年、中村、羽田野、白崎らによって、二次元電子系における熱輸送係数の量子化(量子ネルンスト効果)が理論的に予測されました。
2007年、上述の理論予測によく似た量子ネルンスト効果と思われる現象が、Behniaら(フランス) のグループによって三次元ビスマス単結晶において観測されました。 これを受けて、3次元ビスマス単結晶で大きなネルンスト効果が観測された理由を、電子フォノン相互作用を用いて明らかにしました。 その結果は、実験結果をフィッティングパラメータなしで定量的に再現しました。
参考文献
M. Matsuo, A. Endo, N. Hatano, H. Nakamura, R. Shirasaki, K. Sugihara, Phys. Rev. B 80 (2009) 075313. (Editor's suggestion)
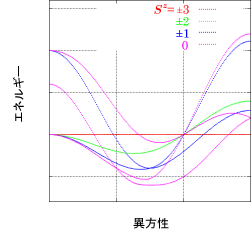
量子多体系において相互作用、異方性などのパラメータを変化させたときに観察されるエネルギー準位の交差現象を、 その系の対称性を用いて理解することが目的です。
量子系のエネルギー縮退はその系の対称性を示唆していることがあります。 例えば水素原子模型のスペクトルは回転対称性によるエネルギー縮退を持つことが有名です。 この回転対称性を記述する角運動量演算子はリー代数sl(2)を生成するため「水素原子模型はsl(2)対称性を持つ」というような言い方をされます。 実際、スペクトルの縮退度はsl(2)の対応する(有限次元)既約表現の次元で与えられます。
近年、ハイゼンベルグスピン鎖に代表されるベーテ仮説法で扱われる一次元量子スピン鎖において、 異方性パラメータの特殊値でエネルギー準位が交差する現象が報告されています。 これはそのパラメータの特殊値において、系がより高い対称性を獲得していることを示唆しています。 実際、その準位交差のいくつかは「系がsl(2)ループ代数という無限次元リー代数の対称性を持つ」ことで理解されます。 sl(2)ループ代数の表現論を用いれば水素原子の場合と同様にスペクトルの縮退度を計算することも可能になります。
参考文献
A. Nishino and T. Deguchi, Phys. Lett. A 356 (2006) 366-370.
久保公式は今から半世紀ほど前に確立した理論であり、スピン系や電子系の物性物理で頻繁に使われています。 ところが実際に久保公式から応答を計算しようと思うと、通常、系のサイズが大きくなるにつれて計算は困難になります。
我々は、巨大ハミルトニアンを持つ量子多体系の久保公式を、任意の温度で数値的厳密に計算できるアルゴリズムを構築しました。 このアルゴリズムは、指数演算子のChebyshev多項式展開と、ランダムベクトルによる対角和の計算を利用して、 計算速度・メモリー使用量ともにO(N)の計算を実現しています。
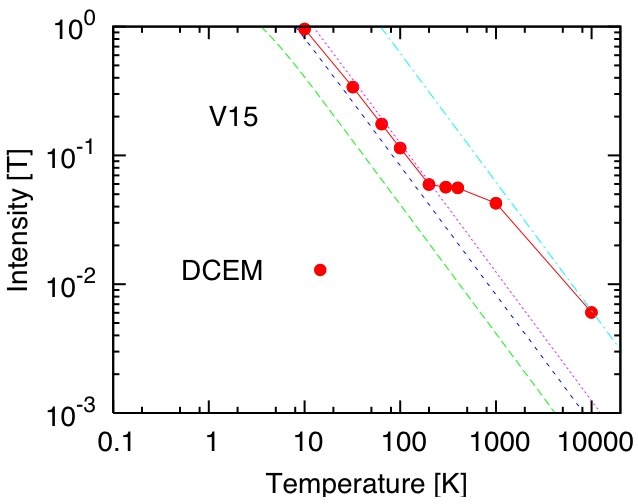
このアルゴリズムはスピン系にも電子系にも適用できますが、ここではスピン系を例にとります。 電子スピン共鳴(ESR)は、静磁場中においたスピン系に振動磁場をかけてエネルギー吸収を測る実験手法ですが、 理論的には久保公式で計算されます。 下図は、V15と呼ばれるナノスケール分子磁性体(ナノ磁石)のESR吸収強度の温度依存性を、 高温から低温にわたって計算した結果です。実験で見られている、200Kあたりでの特異な振舞いが見事に再現されています。 ナノ磁石は、十数個から数十個のスピンからなるナノメートルサイズの磁性体で、 量子コンピュータなどの量子デバイスの素子としても注目されています。
参考文献
M. Machida, T. Iitaka, and S. Miyashita, J. Phys. Soc. Jpn. Suppl. 74 (2005) 107.
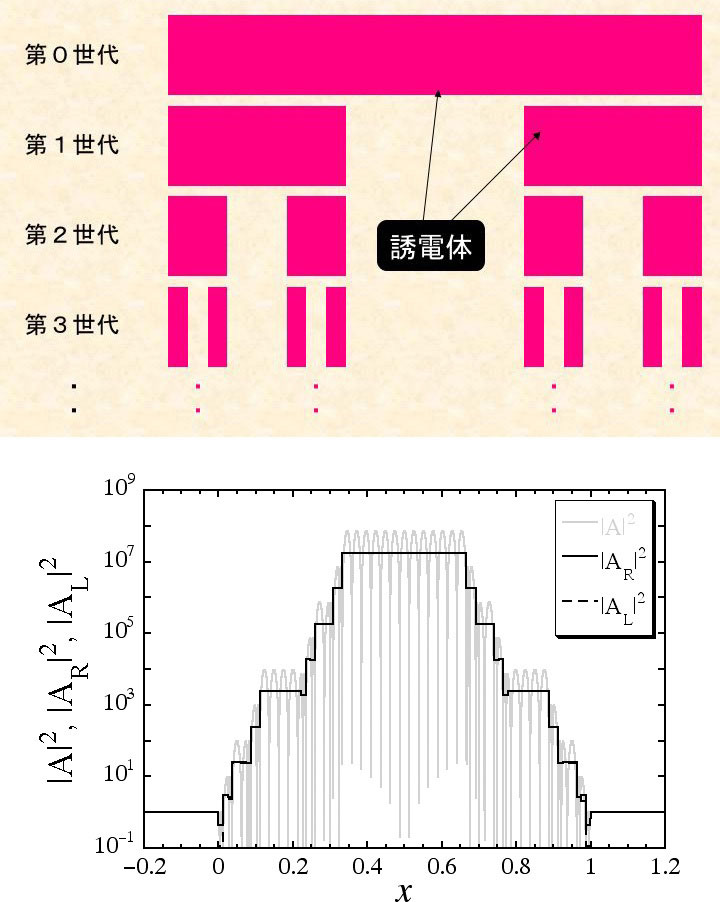
最近、フラクタルな構造を持った誘電体に電磁波を当てて吸収を見る実験が行われました。 それに対応する理論を作って、誘電体の中で電磁波がどのように振る舞うのかを調べました。 フラクタルな構造としては、簡単のために「カントール集合」を使います。 カントール集合とは、線分を3つに分割して中央を取り去る、さらに、のこった部分をそれぞれ3つに分割して中央を取り去る、という作業を繰り返してできるフラクタル構造で、フラクタル次元が0.63です。 ここに電磁波を入射すると、様々な大きさの空洞の中で電磁波が共鳴を起こします。 波長によっては、入射する電磁場の107倍もの強さの電磁場がカントール集合内に発生することがわかりました。
パーコレーションとは注目する要素間に生じる“つながり”に注目した分野です。 この分野の主な興味は、“つながり”がいつ、どのように生じるかです。
これまでに、3次元連続空間に回転楕円体をランダムに分散させた系でのパーコレーションを扱いました。 この系においてパーコレーション転移点fcの回転楕円体の形状に対する依存性をシミュレーションから求めました。 またシミュレーションから得られた転移点fcの振る舞いが、回転楕円体の形状を考慮した領域における局所的な密度を考えることで理解できることが分かりました。
参考文献
S. Akagawa and T. Odagaki, Phys. Rev. E 76 (2007) 051402.