 アンダーソン局在の非エルミート模型による解析(羽田野 直道)
アンダーソン局在の非エルミート模型による解析(羽田野 直道)ボース・アインシュタイン凝縮体の原子間引力相互作用ダイナミクス
 アンダーソン局在の非エルミート模型による解析(羽田野 直道)
アンダーソン局在の非エルミート模型による解析(羽田野 直道)
フラクタルな誘電体中の電磁波の強い共鳴(羽田野 直道)
最近、フラクタルな構造を持った誘電体に電磁波を当てて吸収を見る実験が行われました。それに対応する理論を作って、誘電体の中で電磁波がどのように振る舞うのかを調べました。フラクタルな構造としては、簡単のために「カントール集合」を使います。カントール集合とは、線分を3つに分割して中央を取り去る、さらに、のこった部分をそれぞれ3つに分割して中央を取り去る、という作業を繰り返してできるフラクタル構造で、フラクタル次元が0.63です。ここに電磁波を入射すると、様々な大きさの空洞の中で電磁波が共鳴を起こします。波長によっては、入射する電磁場の107倍もの強さの電磁場がカントール集合内に発生することがわかりました。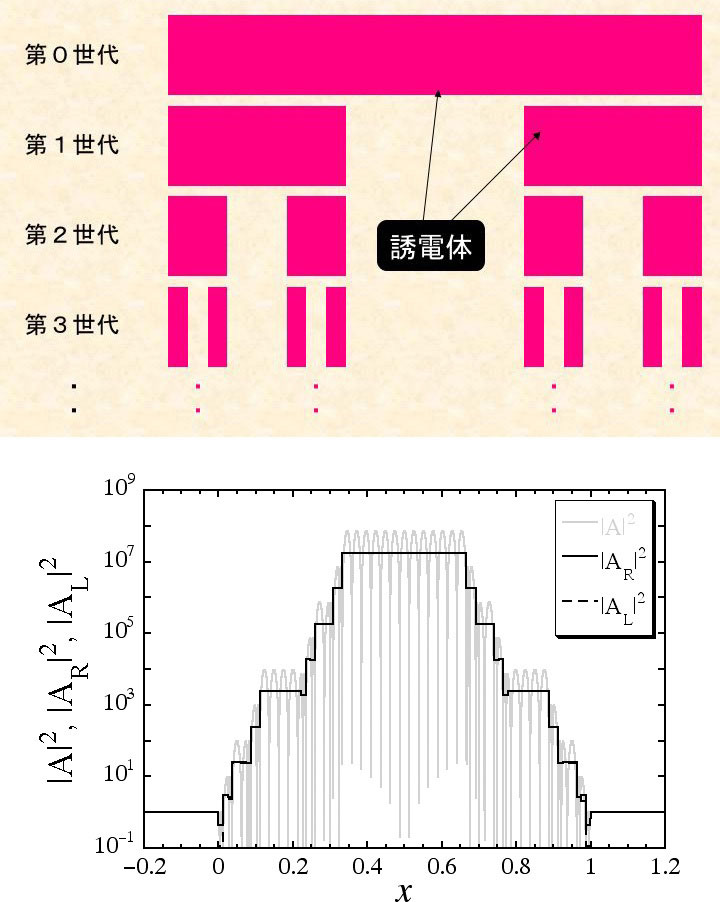
非エルミート行列の固有値分布計算(羽田野 直道)
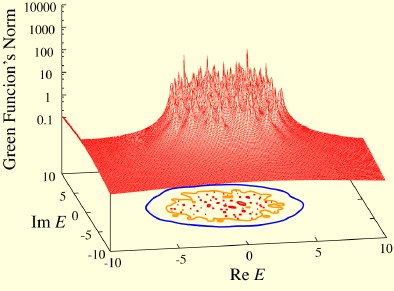
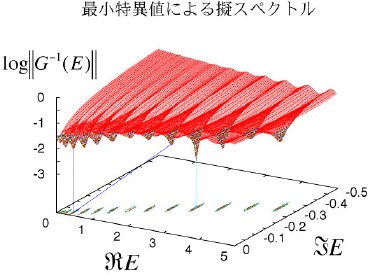
アンダーソン局在や共鳴状態、非平衡モデルの研究のためには、非エルミート行列の固有値分布を知る必要があります。 統計物理的性質を知るためには、非常に大きな(100万×100万行列程度の)非エルミート行列の固有値を計算しなければいけない場合があります。 ところが、現在は巨大な非エルミート行列の固有値分布を効率良く計算するアルゴリズムがありません。 そこで、物理を研究する道具としての数値計算アルゴリズムを開発中です。具体的には、共役傾斜法とランチョス法という2つの方法を組み合わせて、非エルミート行列のグリーン関数のノルム(絶対値のようなもの)を、複素エネルギー平面上で計算します。 下図のような3次元プロットによって固有値分布の構造を知ることができます。
 複雑な運動をする小さな量子系のダイナミクス(町田 学)
複雑な運動をする小さな量子系のダイナミクス(町田 学)
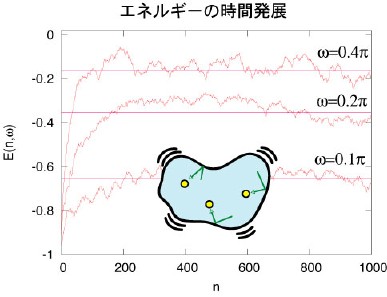
複雑に運動をする量子系を考える。単純な量子系ならばSchroedinger方程式を直接解くことができるだろう。また、粒子数が無限とみなせるほど大きな場合には自由度の多さを逆手にとって熱力学による記述ができる。我々は中途半端な自由度の量子系の外場に対する応答に興味を持っている。このような量子系は、量子ドットやナノ磁石として近年実験的にも作成されるようになった。例えばナノスケールの小さな領域に電子をいくつか閉じ込めてその境界を外から振動させてみよう。内部の電子のエネルギーは古典的にはどんどん上昇するが、今の場合はエネルギーはある値まで上昇すると飽和してしまうことがわかる。我々はランダム行列を用いてこのような系のダイナミクスを調べ、飽和エネルギーと境界の振動数の関係を求めた。つまり、境界の振動のさせ方によって電子が吸収できるエネルギーが変化する。
 ボース・アインシュタイン凝縮体の原子間引力相互作用ダイナミクス(中村 祐一)
ボース・アインシュタイン凝縮体の原子間引力相互作用ダイナミクス(中村 祐一)
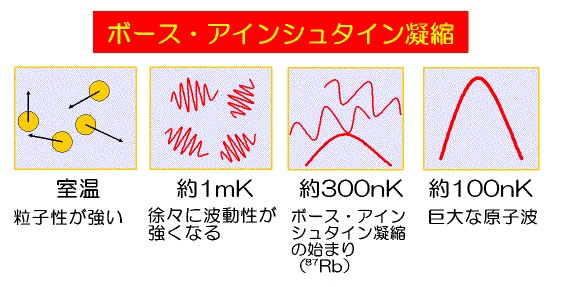
ボース粒子の集合体は、極低温で最低エネルギー準位にまとめて落ち込むことが最近、実験で確認されました。この現象をボース・アインシュタイン凝縮と呼びます。ボース・アインシュタイン凝縮のダイナミクスは,原子間相互作用を平均場エネルギーとして従来のシュレディンガー方程式に付加した、グロス・ピタエフスキー方程式が知られています。しかしながら、原子間に引力が作用する場合には平均場近似の適用限界があり、グロス・ピタエフスキー方程式を超えた新たなモデルの提唱が急務です。現在、引力相互作用のあるボース・アインシュタイン凝縮体のダイナミクスを記述するモデルの考案,及びそれに基づくシミュレーションから、ボース・アインシュタイン凝縮体の物性に新たな知見を与えようとしています。
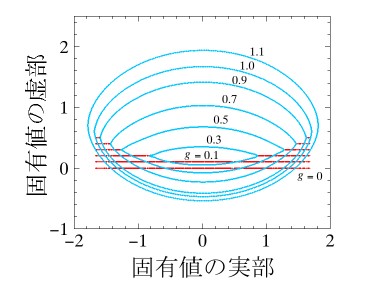
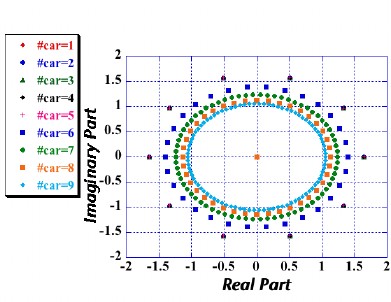
系のエネルギースペクトルのみから相転移現象を視覚的に解釈するための手法の提案を行いました。具体的には従来の時間発展演算子に流れ演算子を摂動として付加した、新しい時間発展演算子を導入します。この手法を離散的交通流モデルであるセルラーオートマトンのルール184に適用して、その固有値分布図を作成しました。下図は、10サイトの固有値分布図です。図から、自由相(車の数が1〜5台)、渋滞相(車の数が6〜9台)の間の相転移を図から視覚的に確認することができます。この手法は,安定状態のみを過不足なく抽出できるので、統計誤差を必然的に生じてしまう従来の交通流シミュレーションよりも精度を飛躍的に向上させることができます。
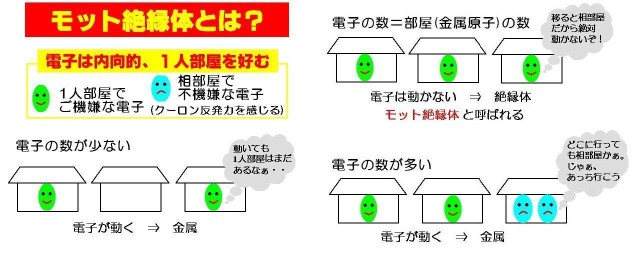
 メゾスコピック系での量子多体効果のある共鳴伝導の解析(笹田 啓太)
メゾスコピック系での量子多体効果のある共鳴伝導の解析(笹田 啓太)
メゾスコピックな素子のコンダクタンスには、共鳴伝導現象が大きく関わっていることがよく知られています。
この共鳴伝導は、素子に導線を接続した開いた系に起こる現象であり、この系での伝導電子は一般的に複素固有値を持ちます。
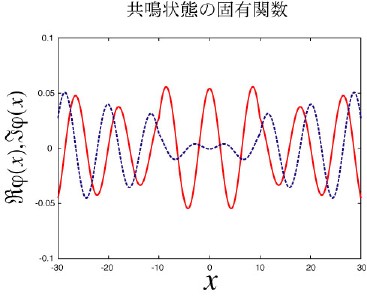
本研究では、開いた系と量子多体効果を同時に解決する新しい計算方法として、遅延グリーン関数の最小特異値による擬スペクトルから共鳴状態の固有値と固有関数を算出することを提案しています。
このとき、有効ハミルトニアンは導線の効果を表す自己エネルギーの項を持つために、非エルミート性を持ちます。そのため、この新しい計算方法が必要となります。
算出した共鳴状態の固有値と固有関数の厳密解から、メゾスコピック系での伝導現象を解析することができます。
現在のところ、相互作用のない一次元の素子に起こる共鳴状態の固有値と固有関数(下図)が得られており、この各々の状態が非線形的に振る舞うコンダクタンスに関与していることが分かっています。
 熱・統計力学の応用としての経済・金融現象の研究(饗場 行洋)
熱・統計力学の応用としての経済・金融現象の研究(饗場 行洋)
近年、統計力学の観点から、経済・金融現象を研究する動きが国内外で盛んになってきている。この背景には、個々の要素の性質がわかっていても、それらが多数集まって系をなすと、個々の性質からは直接想像できない、あらたな現象や機能が発現するという、統計力学における最も興味深い部分が、そのまま経済・金融現象にもあてはまるのではないかという期待がある。例えば、個々の投資家が利益を追求するという行動の特性がわかっていても、その結果として発現する株価や為替の変動にベキ的なゆらぎが現れる現象を、単純には説明することができない。しかし、統計力学的な観点から、ミクロな要素間(ここではディーラー間)の相互作用を規定したモデルを構築することにより、価格変動や所得分布のベキ的な振舞を再現できることがわかってきた。つまり、ミクロとマクロをつなぐ統計力学の手法が、金融・経済現象の理解に大いに役立つと期待されるのである。
我々は、特に複数の為替相場のゆらぎと相互作用に着目して研究をおこなっている。円ドル、ドルユーロ、円ユーロレートをそれぞれ一次元ランダムウォーカーとしてとらえると、それらの重心に復元力が働いているという理解ができることなどがわかってきている(下図)。
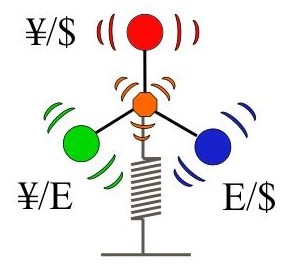
参考文献 Y. Aiba, N. Hatano, H. Takayasu, et al: Physica A310 (2002) 467
ページの先頭へ